15 Máquinas de vetores de suporte
15.1 Classificador de máxima margem
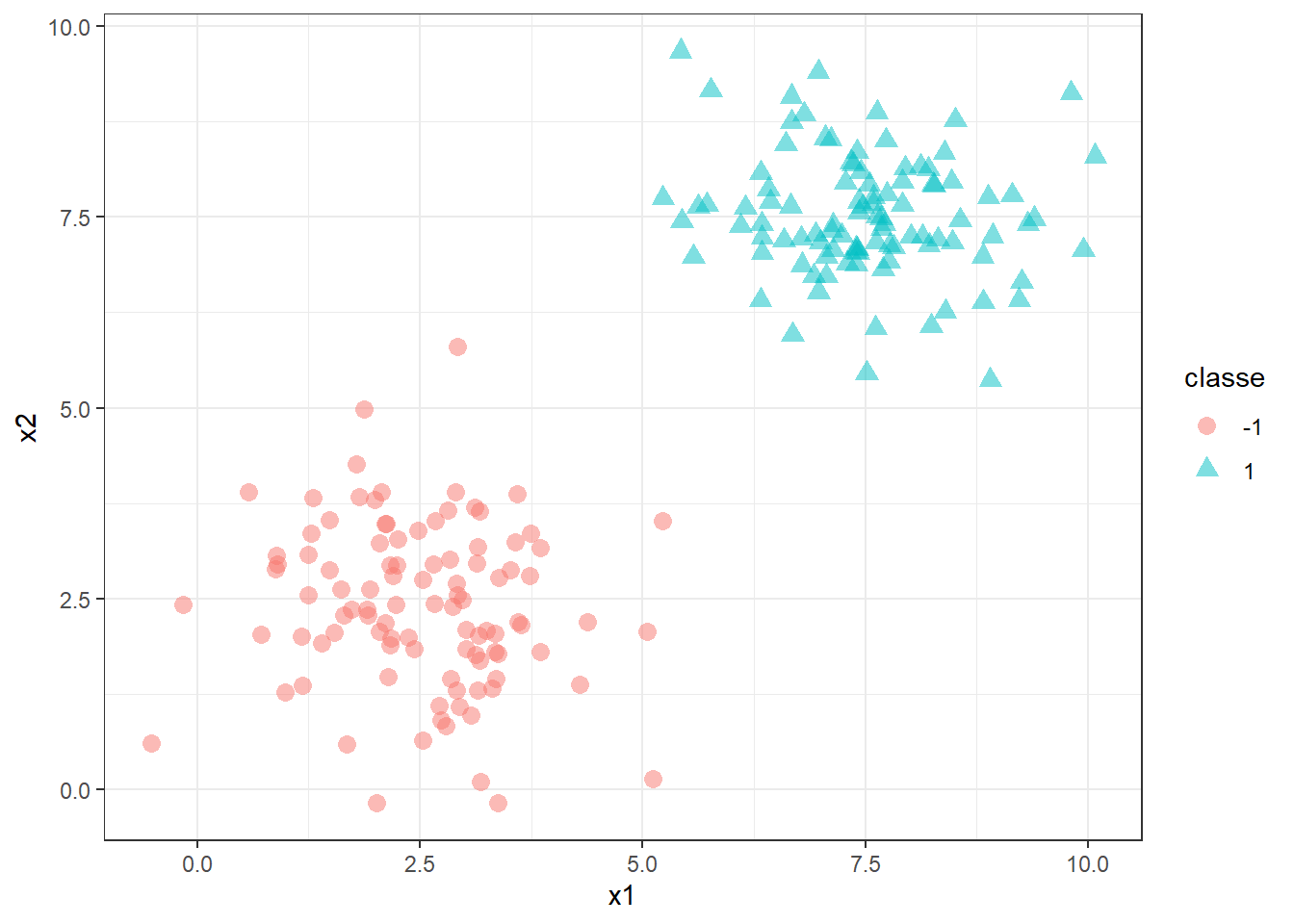
Seja um problema de classificação binário, \(y=\{-1,1\}\) em função de duas variáveis regressores, \(\mathbf{x}=[x_1,x_2]^T\), conforme ilustrado na Figura 15.1.

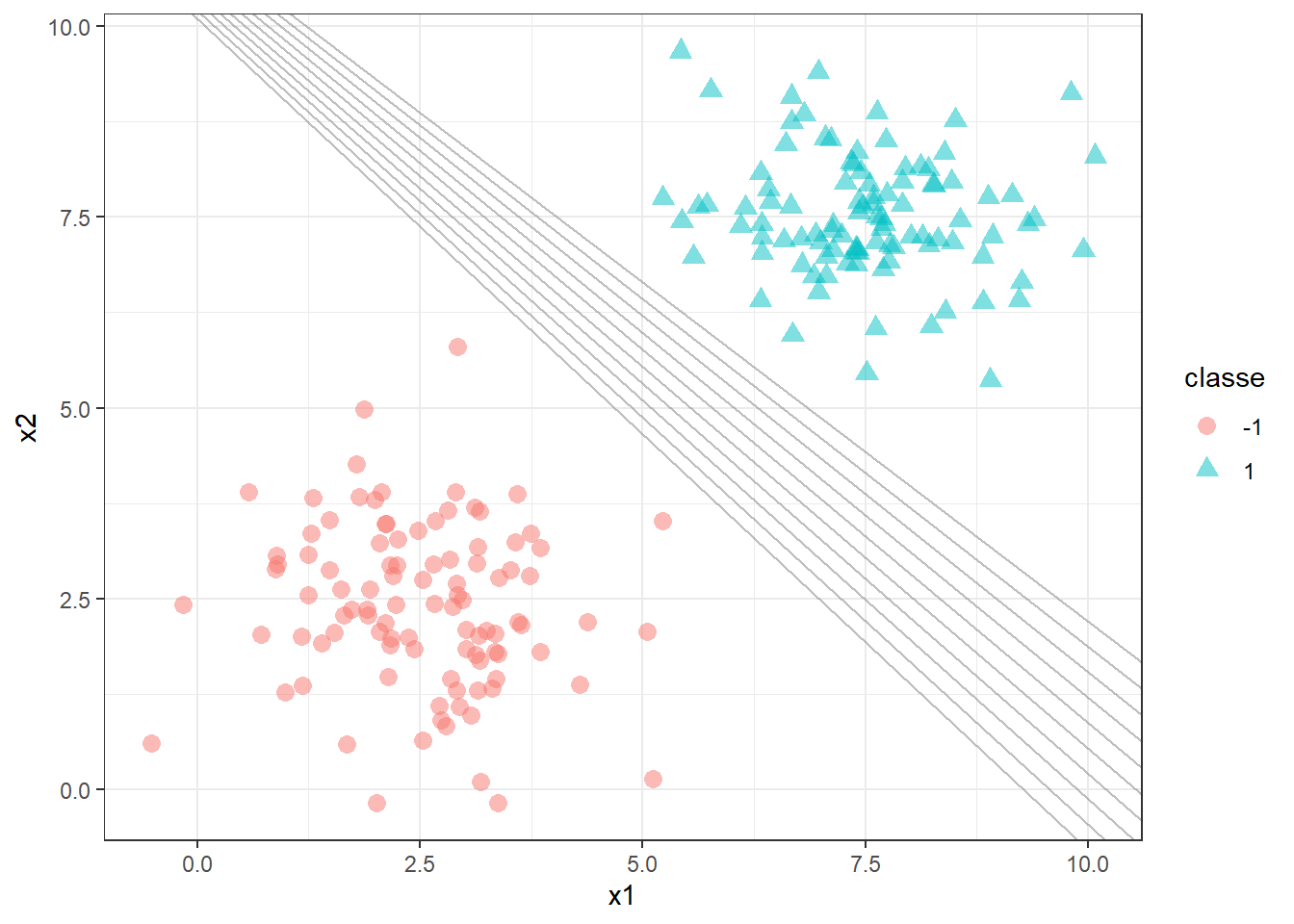
Deseja-se encontrar um classificador, ou hiperplano, que separe tais observações de forma perfeita. Tal hiperplano pode ser representado matematicamente por \(b+\mathbf{w}^T\mathbf{x}=0\). Para \(k=2\), o separador consiste em uma linha, \(b+w_1x_1+w_2x_2 = 0\). Existem infinitas soluções para o problema ilustrado, no qual as classes são ditas perfeitamente separáveis, conforme ilustrado na Figura 15.2.
A regra de classificação usando um hiperplano que faz a classificação perfeita em Equação 15.1.
\[ \begin{align} \text{Se: } b+w_1x_1+w_2x_2>0 \text{, Então: } y=+1 \\ \text{Se: } b+w_1x_1+w_2x_2<0 \text{, Então: } y=-1 \\ \end{align} \tag{15.1}\]
Logo, pode-se garantir que, para qualquer observação \(y_i\) de interesse \(y_i(b+w_1x_1+w_2x_2)>0\), de forma que sempre seja realizada a classificação correta.
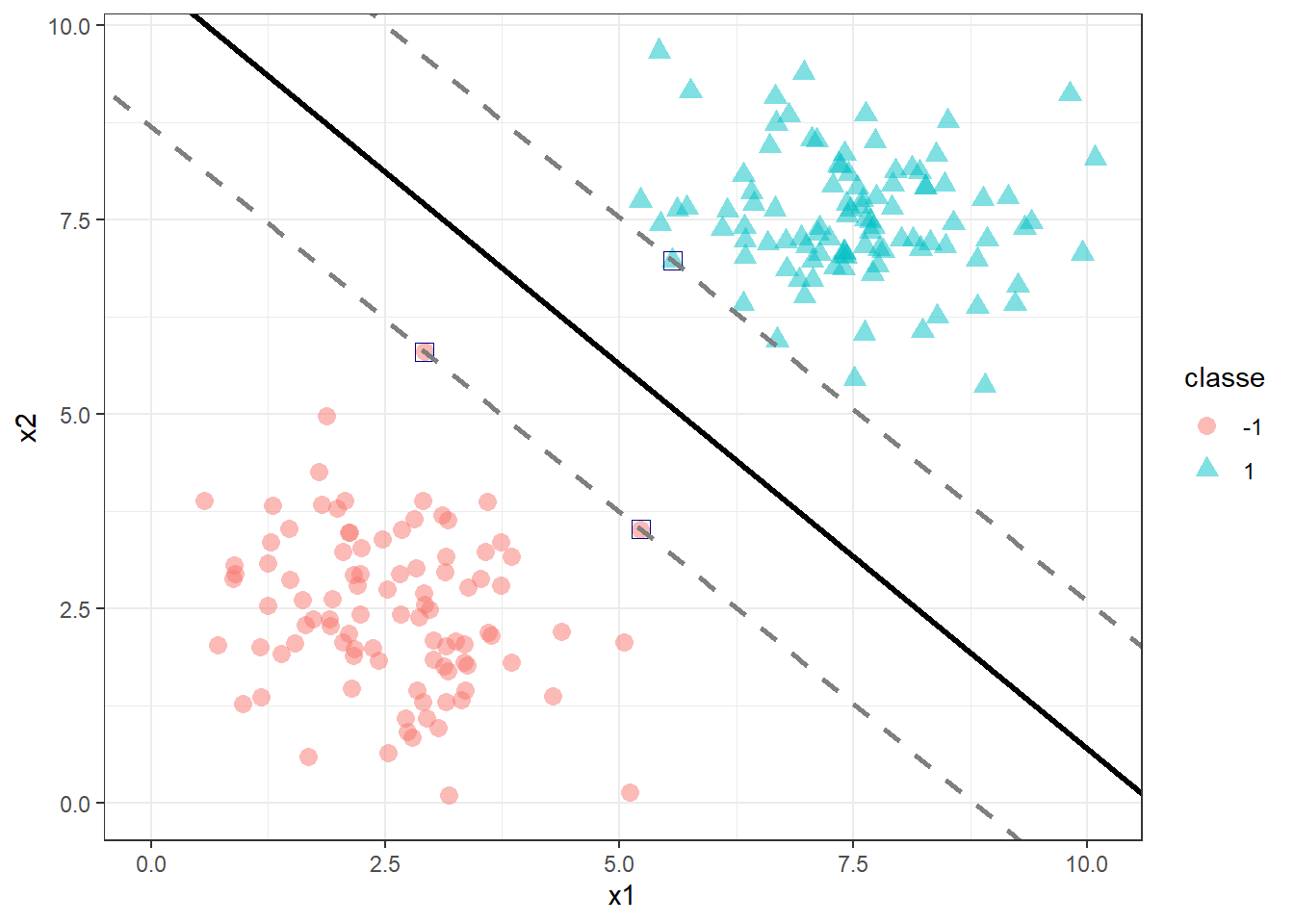
Para garantir a obtenção deste hiperplano, usa-se o conceito de máxima margem. O separador de máxima margem é ilustrado em linha contínua na Figura 15.3. A distância entre ele e as linhas tracejadas paralelas é o que se denomina de margem. Os pontos que se distanciam do hiperplano com distância igual à margem são os vetores de suporte, sendo destacados com quadrado azul. Considerando a margem com comprimento unitário, \(M=1\), pode-se dizer que \(b+w_1x_1+w_2x_2 = 1\), para os pontos que coincidem com a margem superior, enquanto \(b+w_1x_1+w_2x_2 = -1\), para os pontos que interceptam a margem inferior.
Logo, para casos perfeitamente separáveis não há sequer um ponto que satisfaça \(b+w_1x_1+w_2x_2=0\), porém todos os pontos satisfazem a condição em Equação 15.2
\[ \begin{align} \text{Se: } b+w_1x_1+w_2x_2\geq 1 \text{, Então: } y=+1 \\ \text{Se: } b+w_1x_1+w_2x_2\leq-1 \text{, Então: } y=-1, \\ \end{align} \tag{15.2}\]
de forma que \(y_i(b+w_1x_1+w_2x_2)\geq1\). Para encontrar tal hiperplano, busca-se maximizar a margem. Para tal maximização, pode-se considerar a diferença da projeção dos vetores de suporte, no vetor dos coeficientes, \((\mathbf{w}^T\mathbf{x}_a - \mathbf{w}^T\mathbf{x}_b)/||\mathbf{w}|| = 2/||\mathbf{w}||\), onde \(||\mathbf{w}||\) é o comprimento vetorial ou norma de \(\mathbf{w}\), \(||\mathbf{w}||=\sqrt{w_1^2+w_2^2}\). Logo o problema a ser resolvido pode ser formulado conforme Equação 15.3.
\[ \begin{aligned} \text{Max } & \begin{Bmatrix} \frac{2}{||\mathbf{w}||} \end{Bmatrix} \\ \textrm{s.t.: } & \begin{matrix} y_i(\mathbf{w}^T\mathbf{x}_i + b) \geq 1, \forall i=1,...,N\\ \end{matrix} \end{aligned} \tag{15.3}\]
Tal problema é análogo à formulação Equação 15.4. O quadrado da norma facilita a otimização, transformando a função a ser minimizada em convexa.
\[ \begin{aligned} \text{Min } & \begin{Bmatrix} \frac{||\mathbf{w}||^2}{2} \end{Bmatrix} \\ \textrm{s.t.: } & \begin{matrix} y_i(\mathbf{w}^T\mathbf{x}_i + b) \geq 1, \forall i=1,...,N\\ \end{matrix} \end{aligned} \tag{15.4}\]
15.2 Classificador de vetores de suporte
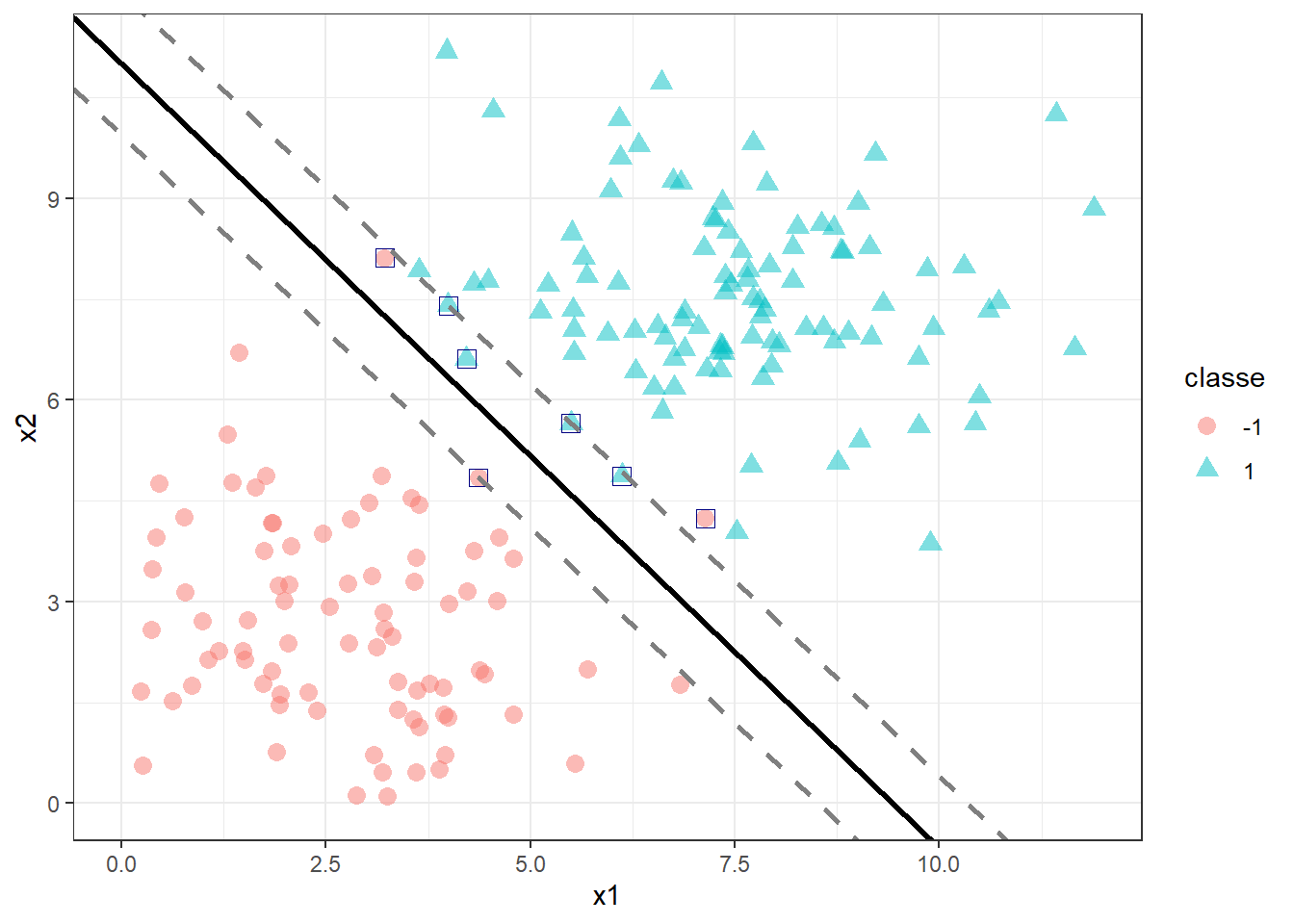
Para casos não perfeitamente separáveis, pode-se permitir que a restrição que até então garantia a classificação perfeita seja violada. A Figura 15.4 ilustra um caso não perfeitamente separável, já com o classificador de vetores de suporte plotado. Pode-se observar que para a classe +1 todos os pontos foram classificados de forma correta, porém ao menos um deles ficou dentro da margem. Já para a classe -1, dois pontos foram classficados incorretamente, sendo um dentro e outro para além da margem oposta.
Para resolver o problema de classificação de forma a obter tal classificador de vetores de suporte, resolve-se o problema da formulação Equação 15.5, onde \(\xi_i\) consiste em variáveis de folga que permitem violar a margem e avaliar se a classificação é correta, de forma que se \(\xi_i = 0\), os pontos são classificados corretamente, se \(\xi_i \leq 1\), a observação está dentro da margem, porém se \(\xi_i > 1\) o ponto está além da margem e classificado erroneamente. Pode-se observar que foi somado um termo na função objetivo, o qual viabiliza minimizar a soma dos termos que violam as margens, \(\sum_i\xi_i\). O parâmetro \(C\) determina o equilíbrio entre a maximização da margem e a minimização dos erros de classificação.
\[ \begin{aligned} \text{Min } & \begin{Bmatrix} \frac{||\mathbf{w}||^2}{2} + C\sum_i\xi_i \end{Bmatrix} \\ \textrm{s.t.: } & \bigg\{ \begin{matrix} y_i(\mathbf{w}^T\mathbf{x}_i + b) \geq 1 - \xi_i, \forall i=1,...,N\\ \xi_i \geq0 \end{matrix} \end{aligned} \tag{15.5}\]
15.3 Máquinas de vetores de suporte
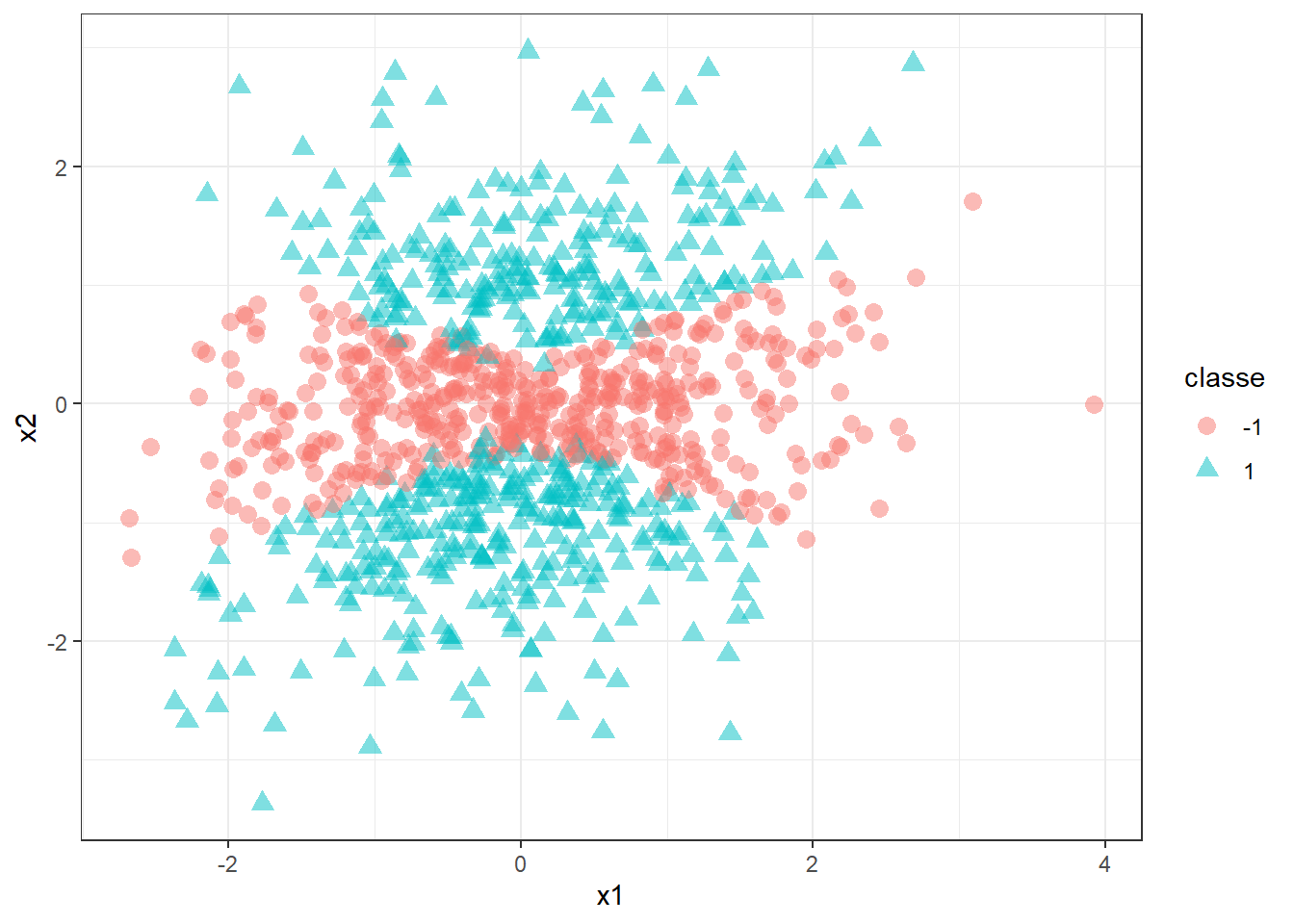
Imagine um caso de classificação onde uma fronteira linear acarretará em baixo desempenho, conforme o ilustrado na Figura 15.5. Neste caso, a não lineariedade dos dados exige a aplicação de um separador mais flexível.
Para construir tal classificador, seja a função lagrangeana correspondente à formulação do classificador de vetores de suporte, a qual comporta objetivos e restrições em uma única função, conforme Equação 15.6.
\[ L=\frac{||\mathbf{w}||^2}{2} + C\sum_i\xi_i - \sum_i\alpha_i(y_i(\mathbf{w}^T\mathbf{x}_i + b) - 1 + \xi_i) -\sum_i\beta_i\xi_i\text{ ,} \tag{15.6}\]
onde \(\alpha_i\) e \(\beta_i\) são os multiplicadores de Lagrange, \(\alpha_i \geq0\) e \(\beta_i\geq0\) , \(i=1,...,N\). Para resolver tal problema deve-se derivar tal função em relação aos parâmetros do modelo e igualar a zero, isto é:
\[ \begin{align} \frac{\partial L}{\partial \mathbf{w}} &= \mathbf{w} - \sum_i\alpha_iy_i\mathbf{x}_i = 0 \\ \frac{\partial L}{\partial b} &= \sum_i\alpha_iy_i =0 \\ \frac{\partial L}{\partial \xi_i} &=C- \alpha_i - \beta_i= 0 \text{, } \forall i=1,...,N \\ \end{align} \tag{15.7}\]
Logo:
\[ \begin{align} \mathbf{w} &= \sum_i\alpha_iy_i\mathbf{x}_i \\ \sum_i\alpha_iy_i &=0 \\ \alpha_i + \beta_i&=C \text{, } \forall i=1,...,N \\ \end{align} \tag{15.8}\]
Substituindo tais resultados na função lagrangeana, pode-se formular o problema dual, conforme Equação 15.9.
\[ \begin{aligned} \text{Max } & \begin{Bmatrix} \sum_i\alpha_i -\frac{1}{2}\alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j \end{Bmatrix} \\ \textrm{s.t.: } & \bigg\{ \begin{matrix} \sum_iy_i\alpha_i=0\\ 0\leq\alpha_i\leq C \text{, } \forall i=1,...,N \end{matrix} \end{aligned} \tag{15.9}\]
A resolução do problema dual em si apenas facilita a otimização dos parâmetros do modelo. Entretanto, é necessário algo mais para obtenção de classificadores que se adaptem a dados não lineares. Para tal, usa-se o chamado truque de kernel. O modelo apresentado inicialmente, \(b+\mathbf{w}^T\mathbf{x}=0\) pode ser reescrito considerando os multiplicadores de lagrange conforme Equação 15.10.
\[ \sum_i\alpha_iy_i\mathbf{x}_i^T\mathbf{x} + b \tag{15.10}\]
Para obter modelos mais flexíveis pode-se substituir a função linear dos vetores de suporte, \(\mathbf{x}_i^T\mathbf{x}\) por uma função mais complexa ou kernel, \(k(\mathbf{x}_i,\mathbf{x})\). A seguir são apresentadas algumas opções.
\[ \begin{align} \text{linear} &: k(\mathbf{x}_i,\mathbf{x}) = \mathbf{x}_i^T\mathbf{x} \\ \text{polinomial} &: k(\mathbf{x}_i,\mathbf{x}) = (\mathbf{x}_i^T\mathbf{x}+1)^d \\ \text{radial} &: k(\mathbf{x}_i,\mathbf{x}) = exp(-\gamma||\mathbf{x}-\mathbf{x}_i||^2) \end{align} \]
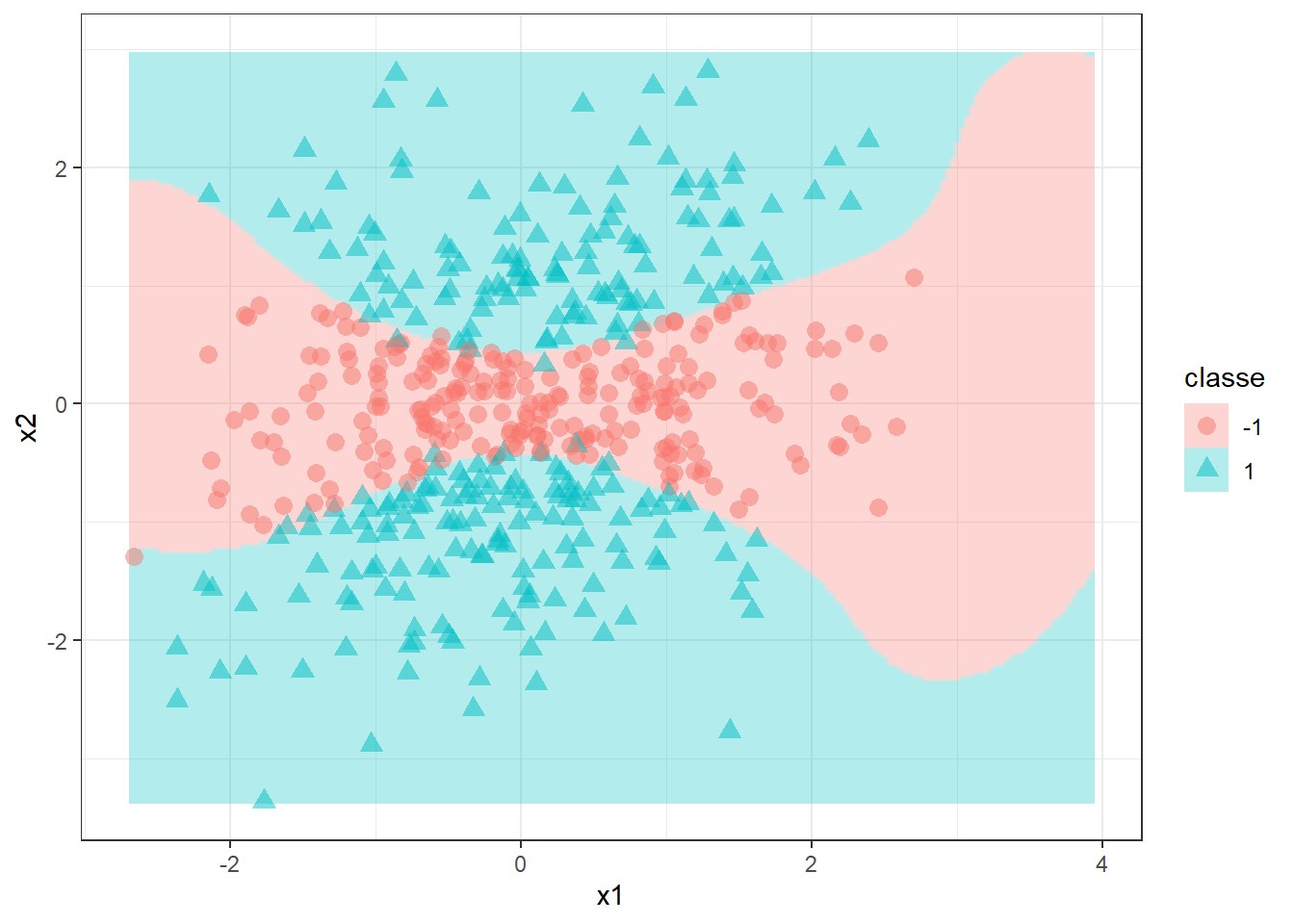
Obviamente é importante considerar o kernel já na otimização, de forma que os hiperparâmetros específicos destes também sejam selecionados adequadamente aos dados. Para o exemplo plotado anteriormente, utilizando um kernel polinomial e metade das observações para treino, obtém-se o classificador plotado na Figura 15.6 com os dados remanescentes.

Para o mesmo exemplo, o kernel radial resulta no classificador plotado na Figura 15.7.
15.4 Implementações em R
A seguir serão expostas as implementações necessárias para obter os resultados do capítulo.
15.4.1 Classificador de máxima margem
Exemplo de dados sintéticos para caso binário perfeitamente separável.
library(ggplot2)
library(e1071)
set.seed(100)
n <- 100
x1 <- matrix(rnorm(n * 2,
mean = 7.5),
ncol = 2)
y1 <- rep(1, n)
x2 <- matrix(rnorm(n * 2,
mean = 2.5),
ncol = 2)
y2 <- rep(-1, n)
x <- rbind(x1, x2)
y <- c(y1, y2)
data <- data.frame(x1 = x[, 1],
x2 = x[, 2],
classe = as.factor(y))Modelagem via SVM.
svm_model <- svm(classe ~ x1 + x2, data = data, kernel = "linear", scale = F, cost = 5)
coefs <- coef(svm_model)
intercept <- -coefs[1]/coefs[3]
slope <- -coefs[2]/coefs[3]Plotando com dados de teste.
# Calcular a margem
margin <- 1 / coefs[3]
# Dados teste
n <- 101
x1t <- matrix(rnorm(n * 2, mean = 7.5), ncol = 2)
y1t <- rep(1, n)
x2t <- matrix(rnorm(n * 2, mean = 2.5), ncol = 2)
y2t <- rep(-1, n)
xt <- rbind(x1t, x2t)
yt <- c(y1t, y2t)
datat <- data.frame(x1 = xt[, 1], x2 = xt[, 2], classe = as.factor(yt))
# visualização
ggplot(datat, aes(x = x1, y = x2, color = classe, pch = classe)) +
geom_point(size = 3, alpha = 0.5) +
geom_abline(slope = slope, intercept = intercept, color = "black", linetype = "solid", size = 1.2) + # Linha separadora
labs(x = "x1",
y = "x2") +
ylim(0,max(data$x2)) +
xlim(0,max(data$x1)) +
theme_bw()15.4.2 Classificador de vetores de suporte
Dados sintéticos para duas classes não separáveis.
set.seed(100)
n <- 100
x1 <- matrix(rnorm(n * 2,
mean = 7.5,
sd=1.7),
ncol = 2)
y1 <- rep(1, n)
x2 <- matrix(rnorm(n * 2,
mean = 2.5,
sd=1.7),
ncol = 2)
y2 <- rep(-1, n)
x <- rbind(x1, x2)
y <- c(y1, y2)
data <- data.frame(x1 = x[, 1],
x2 = x[, 2],
classe = as.factor(y))Modelagem via SVM.
svm_model <- svm(classe ~ x1 + x2,
data = data,
kernel = "linear",
scale = F,
cost = 5)
coefs <- coef(svm_model)
intercept <- -coefs[1]/coefs[3]
slope <- -coefs[2]/coefs[3]Plotando com dados de teste.
set.seed(101)
n <- 100
x1t <- matrix(rnorm(n * 2, mean = 7.5,sd=1.7), ncol = 2)
y1t <- rep(1, n)
x2t <- matrix(rnorm(n * 2, mean = 2.5,sd=1.7), ncol = 2)
y2t <- rep(-1, n)
xt <- rbind(x1t, x2t)
yt <- c(y1t, y2t)
datat <- data.frame(x1 = xt[, 1], x2 = xt[, 2], classe = as.factor(yt))
ggplot(datat, aes(x = x1, y = x2, color = classe, pch = classe)) +
geom_point(size = 3, alpha = 0.5) +
geom_abline(slope = slope, intercept = intercept, color = "black", linetype = "solid", size = 1.2) + # Linha separadora
labs(x = "x1",
y = "x2") +
ylim(0,max(data$x2)) +
xlim(0,max(data$x1)) +
theme_bw()15.4.3 Máquina de vetores de suporte
Caso binário não linear e não perfeitamente separável.
# Parametros para simular dados
library(mvtnorm)
set.seed(14)
m = c(0,0) # vetor de medias
S = matrix(c(1, 0.2, 0.2, 1), 2) # matriz de covariancia
# Simulando dados
dados <- rmvnorm(1000, mean = m, sigma = S)
# funcao para separar classes
f2 <- function(x1,x2) -2*x1^2 + 6*x2^2 - 1
# transformando em data.frame
dados <- data.frame(dados)
colnames(dados) <- c("x1","x2")
# definindo coluna com classes
dados$y <- ifelse(f2(dados$x1,dados$x2) + rnorm(nrow(dados), sd = 0.4) > 0, 1, -1)
dados$y <- as.factor(dados$y)
# dados de treino e teste
set.seed(1)
tr <- round(0.5*nrow(dados))
treino <- sample(nrow(dados), tr, replace = F)
dados.treino <- dados[treino,]
dados.teste <- dados[-treino,]Validação cruzada e modelagem com kernel polinomial.
ctrl <- tune.control(
sampling='cross', # Do cross-validation (the default)
cross=10, # Num folds (default = 10)
nrepeat=2) # Num repeats (default is 1)
train.grid <- list(cost=2^(-2:5), gamma=2^seq(-1, 1, by=.5))
# validacao cruzada e grid search para definir C
set.seed(1)
tune.out <- tune(svm, y~.,
data = dados.treino,
kernel = "polynomial",
degree = 2,
ranges = list(cost=c(0.001, 0.01, 0.1, 1, 5,10, 100)))
# modelo com C otimo
svm1 <- svm(y~.,
data = dados.treino,
kernel = "polynomial",
cost = tune.out$best.parameters,
degree = 2,
scale = FALSE)Visualizando modelo com dados de teste.
### visualizacao
grid <- expand.grid(x1 = seq(min(c(dados.treino$x1, dados.teste$x1)),
max(c(dados.treino$x1, dados.teste$x1)), length = 200),
x2 = seq(min(c(dados.treino$x2, dados.teste$x2)),
max(c(dados.treino$x2, dados.teste$x2)), length = 200))
grid$class <- predict(svm1, grid)
## Teste
ggplot() +
geom_raster(aes(x = grid$x1, y = grid$x2, fill = grid$class),
alpha = 0.3, interpolate = T) +
geom_point(aes(x = dados.teste$x1, y = dados.teste$x2,
color = dados.teste$y,
shape = dados.teste$y), size = 3, alpha=.5) +
labs(x = "x1", y = "x2", col = "classe",
shape = "classe", fill = "classe") + theme_bw()Desempenho para dados de teste.
pred_teste1 <- predict(svm1, newdata = dados.teste, type = "response")
cm <- table(dados.teste$y,pred_teste1)
cmacc <- sum(diag(cm))/sum(cm)
accspec <- cm[2,2]/sum(cm[2,])
specsens <- cm[1,1]/sum(cm[1,])
sensValidação cruzada e modelagem com kernel radial.
# validacao cruzada e grid search para definir C e gamma
set.seed(1)
tune.out <- tune(svm, y~.,
data = dados.treino,
kernel = "radial",
degree = 2,
ranges = train.grid)
# modelo com C otimo
svm2 <- svm(y~.,
data = dados.treino,
kernel = "radial",
cost = tune.out$best.parameters[1],
gamma = tune.out$best.parameters[2],
scale = FALSE)Visualizando modelo com dados de teste.
grid$class <- predict(svm2, grid)
## Teste
ggplot() +
geom_raster(aes(x = grid$x1, y = grid$x2, fill = grid$class),
alpha = 0.3, interpolate = T) +
geom_point(aes(x = dados.teste$x1, y = dados.teste$x2,
color = dados.teste$y,
shape = dados.teste$y), size = 3, alpha=.5) +
labs(x = "x1", y = "x2", col = "classe",
shape = "classe", fill = "classe") + theme_bw()Desempenho para dados de teste.
pred_teste2 <- predict(svm2, newdata = dados.teste, type = "response")
cm2 <- table(dados.teste$y,pred_teste2)
cm2acc2 <- sum(diag(cm2))/sum(cm2)
acc2spec2 <- cm2[2,2]/sum(cm2[2,])
spec2sens2 <- cm2[1,1]/sum(cm2[1,])
sens2Referências
Boser, B. E., Guyon, I. M., & Vapnik, V. N. (1992, July). A training algorithm for optimal margin classifiers. In Proceedings of the fifth annual workshop on Computational learning theory (pp. 144-152).
Cortes, C., & Vapnik, V. (1995). Support-vector networks. Machine learning, 20, 273-297.
Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.
Vapnik, V. N. (1999). An overview of statistical learning theory. IEEE transactions on neural networks, 10(5), 988-999.
Vapnik, V. (2013). The nature of statistical learning theory. Springer science & business media.