14  Classificação via análise discriminante

14.1 Análise discriminante linear binária simples

A análise linear discriminante é um método de estatística multivariada concebido por Fisher, usado para classificação. Seja um problema de classificação binária de um supervisor de interesse, \(y=\{1,2\}\) em função de uma variável independente, \(x \in \mathcal{R}\). Pelo teorema de Bayes, pode-se trabalhar a probabilidade condicional de \(y\) pertencer a uma classe de interesse dado um valor de \(x\), por exemplo, \(p(y=1|x)\), conforme Equação 14.1.

\[ p(y=1|x) = \frac{p(x|y=1)p(y=1)}{p(x)} \tag{14.1}\]

Onde \(p(x|y=1)\) é a verossimilhança que consiste na probabilidade de \(x\) dado que \(y=1\) é verdade, podendo ser aproximada pela função densidade de probabilidade de \(x\) dado que \(y=1\). \(p(y=1)\) seria a probabilidade de \(y\) pertencer à classe 1, a qual pode ser estimada a partir da proporção dos dados de treino correspondentes. Por fim, \(p(x)\) seria a probabilidade da variável independente, que pode ser aproximada pela lei da probabilidade total e será constante e independente das classes. Tomando a distribuição normal, a verossimilhança pode ser aproximada conforme Equação 14.2, onde \(\mu_1\) e \(\sigma_1\) são, respectivamente, a média e o desvio-padrão da distribuição de \(x\) dado que \(y=1\), os quais podem ser aproximados por dados amostrais.

\[ p(x|y=1)=f_1(x)=\frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{1}{2}\bigl(\frac{x-\mu_1}{\sigma_1}\bigr)^2} \tag{14.2}\]

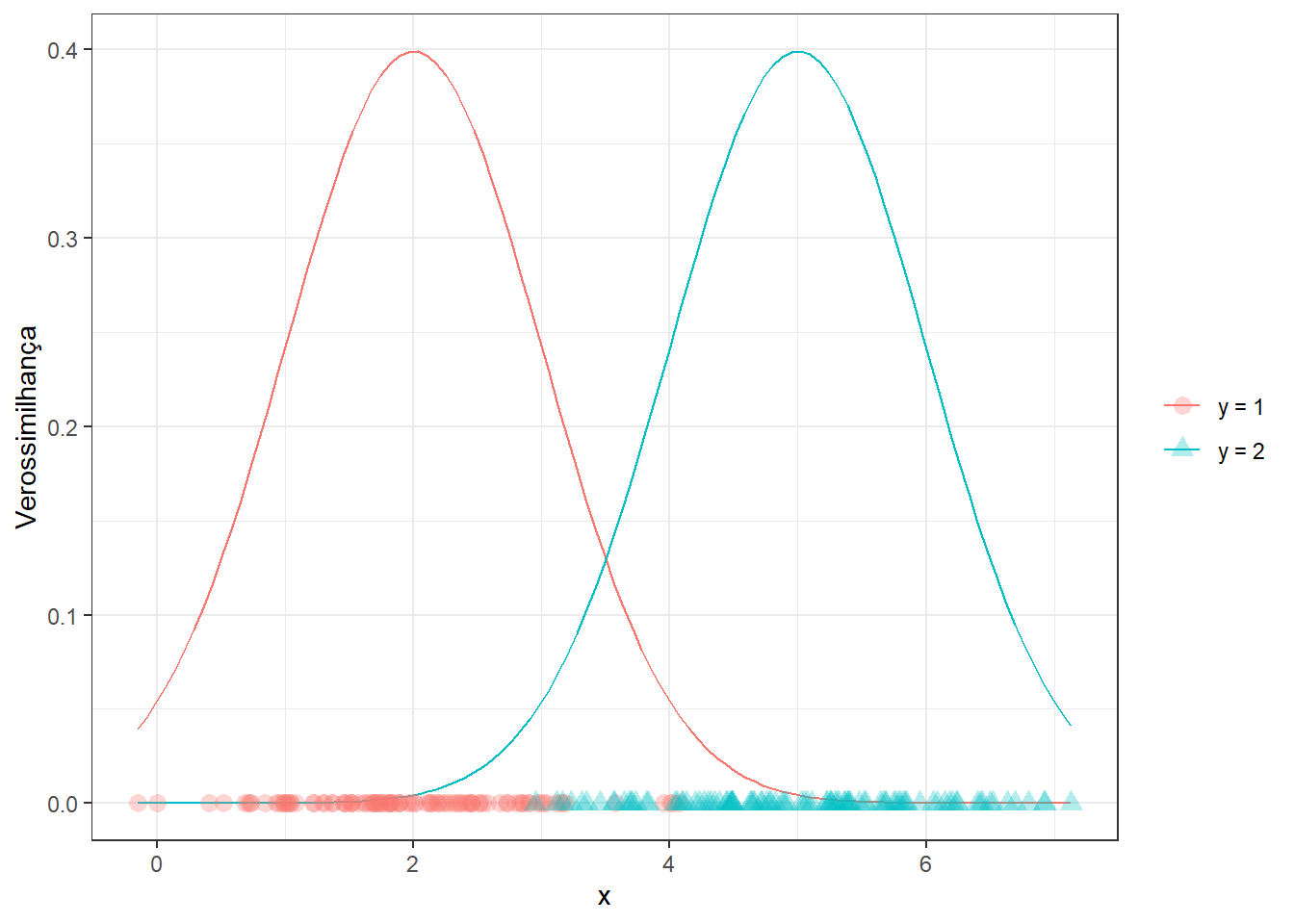
A análise discriminante linear considera que as distribuições de \(x\) para as classes de interesse apresentam igual variabilidade, \(\sigma=\sigma_1=\sigma_2\). No caso de problemas de classificação deseja-se ao final saber o valor de \(x\) que discrimina as classes de interesse. A Figura 14.1 exibe dados de duas classes distintas em função de uma única variável regressora e as densidades teóricas correspondentes de \(x\) para cada uma das classes.

Figura 14.1: Observações e densidades teóricas de duas classes em função de uma variável

Pode-se observar que a análise discriminante linear considera \(\sigma_1=\sigma_2=\sigma\), ou seja, o desvio-padrão e, consequentemente, a variância é constante para as classes. Aplicando os conceitos explicados na formulação inicial obtém-se a Equação 14.3.

\[ p(y=1|x) = \frac{p(y=1)\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\bigl(\frac{x-\mu_1}{\sigma}\bigr)^2}}{p(x)} \tag{14.3}\]

Assim como na regressão logística, pode-se usar o log da razão de chance para facilitar a discriminação, conforme Equação 14.4. O logaritmo facilita a separação dos produtos e da razão em soma e subtração, respectivamente.

\[ \begin{align} \text{ln } \biggl(\frac{p(y=1|x)}{p(y=2|x)}\biggr) & = \text{ln } \biggl(\frac{f_1(x)}{f_2(x)}\frac{p(y=1)}{p(y=2)}\biggr) \\ & =\text{ln } \frac{f_1(x)}{f_2(x)}+ \text{ln }\frac{p(y=1)}{p(y=2)} \\ \end{align} \tag{14.4}\]

Supondo o equilíbro entre as classes, \(\text{ln }\frac{p(y=1)}{p(y=2)} = 0\). Logo, obtém-se o resultado da Equação 14.5.

\[ \begin{align} \text{ln } \biggl(\frac{p(y=1|x)}{p(y=2|x)}\biggr) & = \text{ln } \frac{\frac{1}{\sqrt{2\pi}\sigma}e^\frac{-(x-\mu_1)^2}{\sigma}}{\frac{1}{\sqrt{2\pi}\sigma}e^\frac{-(x-\mu_2)^2}{\sigma}} \end{align} \tag{14.5}\]

Fazendo as devidas simplificações, obtém-se a Equação 14.6.

\[ \begin{align} \text{ln } \biggl(\frac{p(y=1|x)}{p(y=2|x)}\biggr) & = \frac{\mu_2^2-\mu_1^2}{2\sigma^2} + x\frac{\mu_1-\mu_2}{\sigma^2} \end{align} \tag{14.6}\]

Se o log da razão de chance for maior que 0, então classifica-se \(y\) como pertencente à classe 1. Se, ao contrário, for menor que 0, \(y\) é classificado para a classe 2. As estimativas da média condicional e da variância comum são calculadas conforme Equação 14.7, onde \(c = {1,2}\) e o número de classes \(C=2\) para o caso binário.

\[ \begin{align} \hat{\mu}_c & = \frac{1}{n_c}\sum_{i:y_i=c}x_i \\ \hat{\sigma}^2 &=\frac{1}{n-C}\sum_{c=1}^C\sum_{i:y_i=c}(x_i-\hat{\mu}_i)^2 \\ \end{align} \tag{14.7}\]

Considerando o log da razão de chance nulo e resolvendo para \(x\) a Equação 14.6, pode-se obter a fronteira de decisão pela Equação 14.8, que no caso simples consiste na média das médias da variável independente condicional às classes.

\[ x=\frac{\mu_1+\mu_2}{2} \tag{14.8}\]

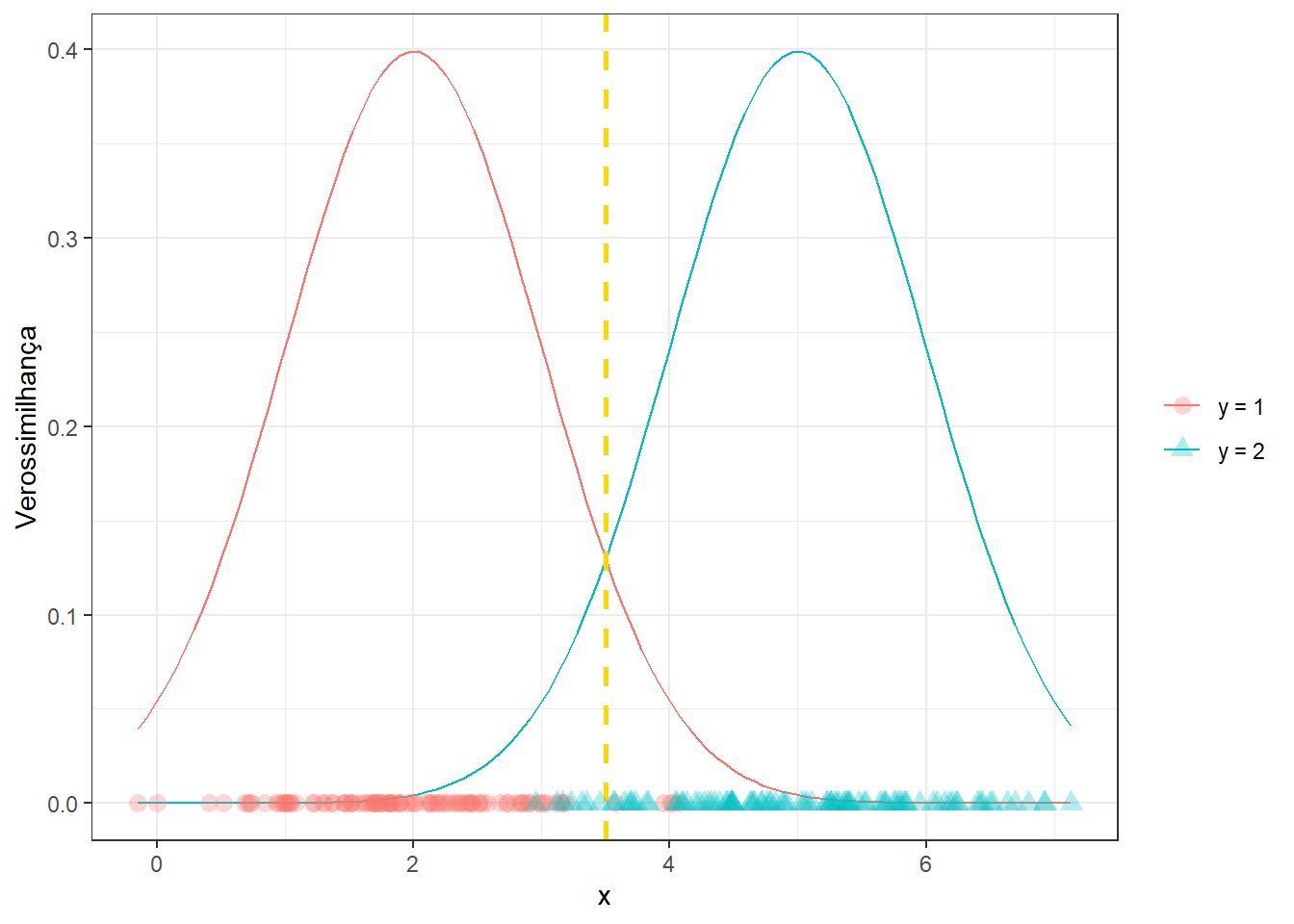
Neste sentido, pode-se retomar o exemplo plotado anteriormente com a fronteira de decisão na Figura 14.2. Pode-se observar que a fronteira maximiza as probabilidades de verdadeiros positivos e negativos e minimiza as probabilidades de falsos positivo e negativo.

Figura 14.2: Fronteira de decisão para análise discriminante linear simples

14.1.1 Analogia com a regressão logística

Tomando novamente o logaritmo da razão de chance, os coeficientes de regressão logística podem ser definidos com base nestes parâmetros segundo a Equação 14.9, de forma que os resultados dos dois classificadores são análogos.

\[ \begin{align} \beta_0 &= \frac{\mu_2^2-\mu_1^2}{2\sigma^2} \\ \beta_1 &= \frac{\mu_1-\mu_2}{\sigma^2} \\ \end{align} \tag{14.9}\]

14.1.2 Função linear discriminante de Ficher

Fisher também determinou uma função linear discriminante, a qual visa maximizar a variância entre os grupos relativamente à variância comum dentro dos grupos. A função é expressa na Equação 14.10, consistindo no termo do log da razão de chance que contém \(x\).

\[ u(x) = \frac{\mu_1-\mu_2}{\sigma^2}x \tag{14.10}\]

14.2 LDA para \(k\) variáveis independentes e duas classes

Seja o caso onde deseja-se realizar uma classificação binária em função de \(k\) variáveis independentes, \(x_1, x_2, ..., x_k\). Tais variáveis podem ser condensadas em um vetor \(k\)-dimensional, \(\mathbf{x} = [x_1, x_2, ..., x_k]^T\). O teorema de Bayes pode ser novamente usado, porém a verossimilhança será expressa pela função densidade de probabilidade multivariada, que no caso normal, considerando a classe \(y=1\), consiste na Equação 14.11.

\[ p(\mathbf{x}|y=1)=f_1(\mathbf{x})=\frac{1}{(2\pi)^{k/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(\mathbf{x}-\mu_1)^T\Sigma^{-1}(\mathbf{x}-\mu_1)} \tag{14.11}\]

Na função de densidade normal multivariada, \(\mu_1\) consiste no vetor de médias para as \(k\) variáveis independentes, condicional a \(y=1\), \(\mu_1 = [\bar{x}_{1,y=1},\bar{x}_{2,y=1},...,\bar{x}_{k,y=1}]^T\) e \(\Sigma\) consiste na matriz de covariância comum às duas classes, segundo Equação 14.12.

\[ \Sigma = \biggl[ \begin{matrix} \sigma_1^2 & \sigma_{12} \\ \sigma_{21} & \sigma_2^2 \end{matrix} \biggr] \tag{14.12}\]

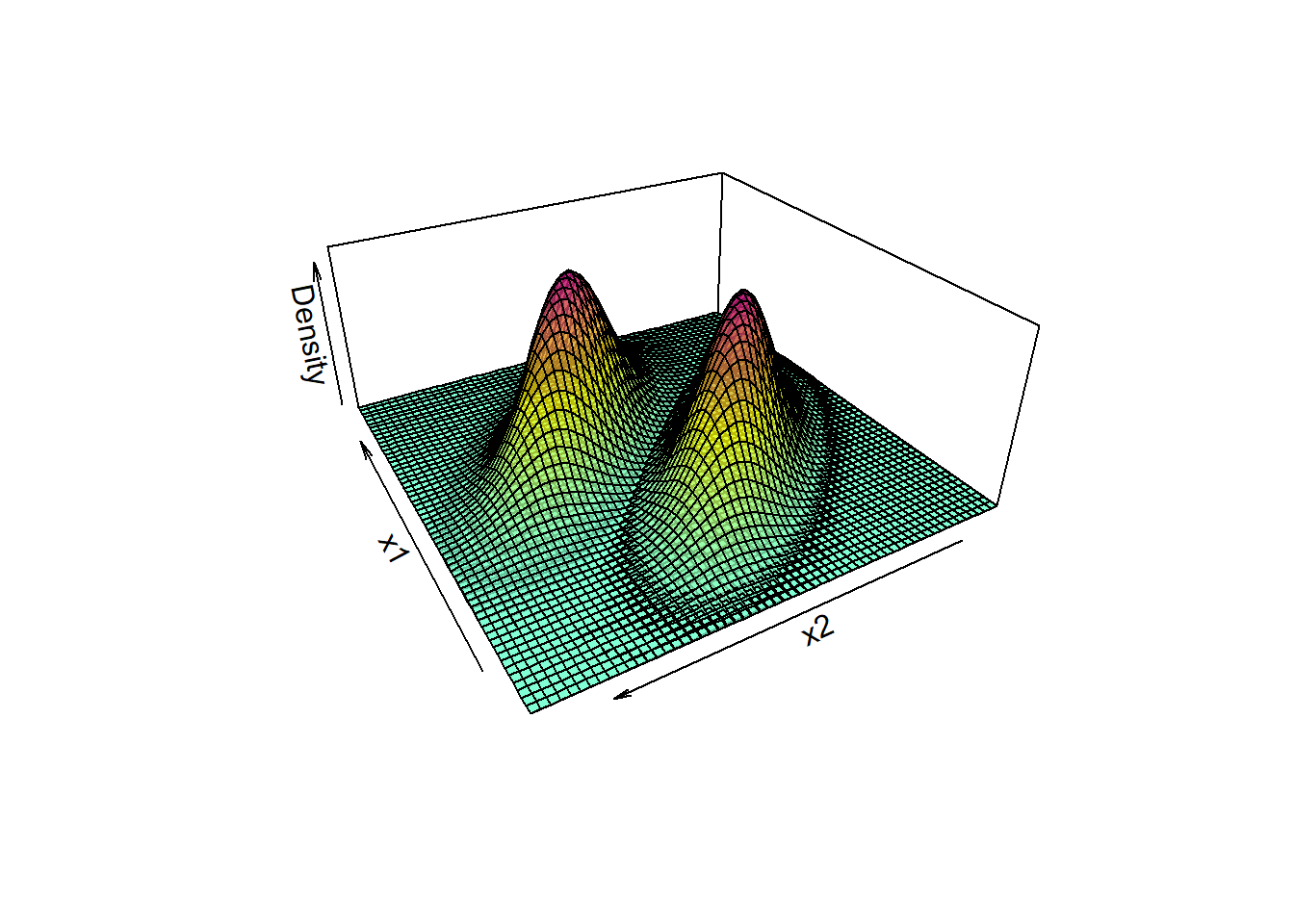
A Figura 14.3 plota densidades bivariadas de dados de um caso de classificação binária.

Figura 14.3: Densidades teóricas de duas classes em função de duas variáveis

Sem a necessidade de repetir as deduções anteriores, pode-se escrever o log da razão de chance para o caso multivariado conforme Equação 14.13. Se o logit for maior que 0, então y=1. De forma análoga pode-se considerar a função discriminante como parte do logit que é função de \(\mathbf{x}\).

\[ \text{ln } \biggl(\frac{p(y=1|\mathbf{x})}{p(y=2|\mathbf{x})}\biggr) = (\mu_1-\mu_2)^T\Sigma^{-1}\mathbf{x} - \frac{1}{2}(\mu_1-\mu_2)^T\Sigma^{-1}(\mu_1+\mu_2) \tag{14.13}\]

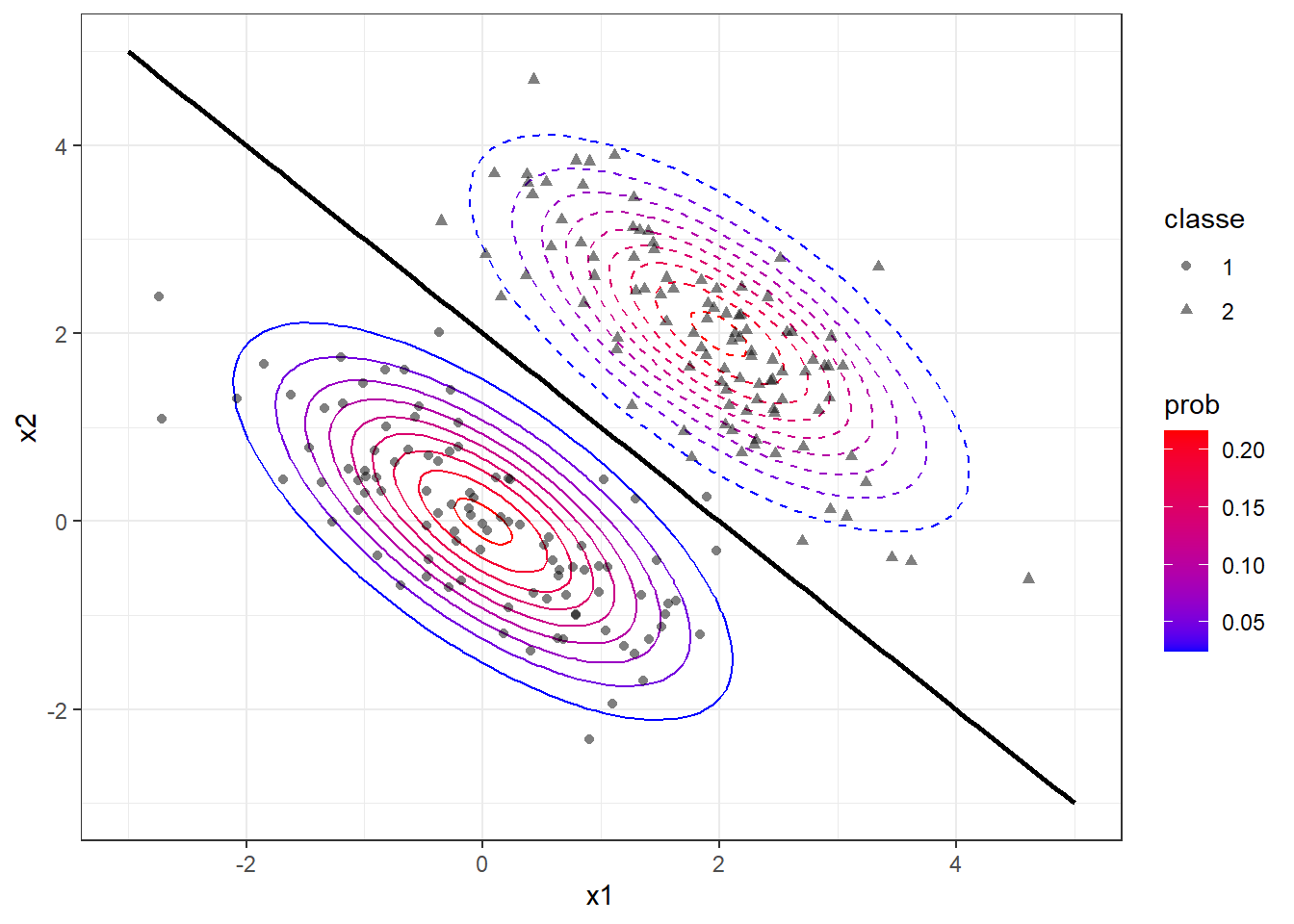
Na Figura 14.4 o exemplo plotado na Figura 14.3 é novamente exibido em curvas de contorno com a fronteira obtida para discriminar as classes, além dos dados amostrais considerados.

Figura 14.4: Fronteira de discriminação binária para caso em função de duas variáveis

A função discriminante linear para o caso de múltiplas variáveis independentes e duas classes é definida na Equação 14.14.

\[ u(x) = (\mu_1-\mu_2)\Sigma^{-1}\mathbf x \tag{14.14}\]

14.3 LDA para \(k\) variáveis independentes e três ou mais classes

No caso de três ou mais classes é conveniente trabalhar uma função discriminante a partir do teorema de Bayes, sem uso da razão de chance. Tomando apenas o numerador, uma vez que o denominador é constante à todas as classes, tem-se para a \(c\)-ésima classe a probabilidade condicional de pertencer a \(c\) conforme ?eq-eq-pcondc, \(c=1,2,...,C\).

\[ p(y=c|\mathbf{x}) =p(\mathbf{x}|y=c)p(y=c) \tag{14.15}\]

Aplicando o logaritmo, pode-se eliminar o segundo termo da soma dos logs, uma vez que este será igual para todas as classes em casos de igualdade de observações entre estas, \(n_1,n_2,...,n_c\). Após aplicar a verossimilhança pode-se também eliminar o termo \(\frac{1}{(2\pi)^{k/2}|\Sigma|^{1/2}}\), uma vez que será constante para todas as classes.

\[ \begin{align} \text{ln }(p(y=c|\mathbf{x})) & =\text{ln } (p(\mathbf{x}|y=c)p(y=c)) \\ & = \text{ln } p(\mathbf{x}|y=c) + \not{\text{ln }p(y=c)} \\ & \simeq \text{ln } \frac{1}{(2\pi)^{k/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(\mathbf{x}-\mu_c)^T|\Sigma|^{-1}(\mathbf{x}-\mu_c)} \\ \end{align} \tag{14.16}\]

Logo, a função discriminante para a c-ésima classe pode ser deduzida conforme Equação 14.14, sendo o primeiro termo eliminado após a expansão dos produtos, visto que não depende da classe.

\[ \begin{align} u(\mathbf{x}) & = -\frac{1}{2}(\mathbf{x}-\mu_c)^T|\Sigma|^{-1}(\mathbf{x}-\mu_c) \\ & = \not{-\frac{1}{2}\mathbf{x}^T\Sigma^{-1}\mathbf{x}} + \frac{1}{2}\mu_c^T\Sigma^{-1}\mathbf{x} + \frac{1}{2}\mathbf{x}^T\Sigma^{-1}\mu_c-\frac{1}{2}\mu_c^T\Sigma^{-1}\mu_c \\ u(\mathbf{x}) & = \mathbf{x}^T\Sigma^{-1}\mu_c-\frac{1}{2}\mu_c^T\Sigma^{-1}\mu_c \\ \end{align} \]

Considere o famoso conjunto de dados Iris, comumente atribuído a Fisher, o qual contém medições em centímetros do comprimento e largura de pétalas e sépalas de três distintas espécies de orquídeas. A Tabela 14.1 exibe as primeiras linhas de tal conjunto de dados.

Tabela 14.1: Observações do conjunto de dados Iris

Sepal.Length	Sepal.Width	Petal.Length	Petal.Width	Species
5.1	3.5	1.4	0.2	setosa
4.9	3.0	1.4	0.2	setosa
4.7	3.2	1.3	0.2	setosa
4.6	3.1	1.5	0.2	setosa
5.0	3.6	1.4	0.2	setosa
5.4	3.9	1.7	0.4	setosa

Pode-se plotar aos pares tais variáveis considerando também as distribuições individuais e correlações separadas por espécies.

Figura 14.5: Diagramas de dispersão e correlações aos pares para o conjunto de dados Iris

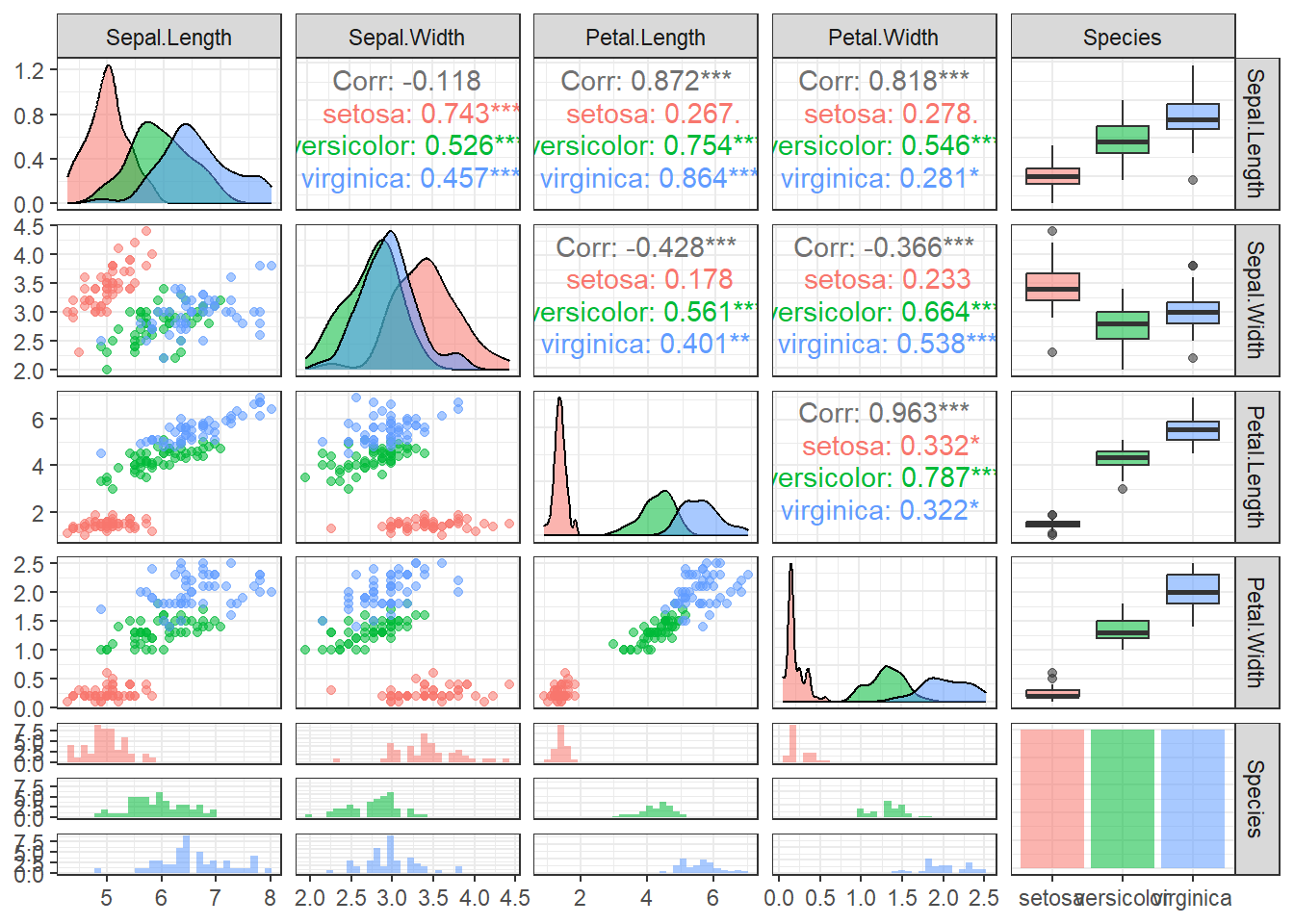
Tomando aleatoriamente 75% das observações para treino, um modelo obtido via LDA é obtido conforme segue. O resultado da modalegam expõe as probabilidades à priori, que consiste nas proporções de observações cada classe segundo dados de treino, os vetores de médias de cada classe, considerando as variáveis independentes e os coeficientes para discriminação linear, além da importância destes para discriminação (proporção do traço).

Call:
lda(Species ~ ., data = data.treino)

Prior probabilities of groups:
    setosa versicolor  virginica 
 0.3303571  0.3214286  0.3482143 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa         5.008108    3.424324     1.459459   0.2486486
versicolor     5.955556    2.775000     4.313889   1.3277778
virginica      6.684615    2.984615     5.620513   2.0256410

Coefficients of linear discriminants:
                    LD1        LD2
Sepal.Length  0.7777911 -0.3750326
Sepal.Width   1.6113137 -1.9569617
Petal.Length -2.1931112  1.0793649
Petal.Width  -2.6770295 -2.8163545

Proportion of trace:
   LD1    LD2 
0.9912 0.0088 

Aplicando tal modelo aos dados de teste, obtém-se a seguinte matriz de confusão. Pode-se observar que o modelo acertou 100% das classificações de teste.

            pred
y            setosa versicolor virginica
  setosa         13          0         0
  versicolor      0         14         0
  virginica       0          0        11

14.4 Análise discriminante quadrática

A análise discriminante quadrática é útil para casos onde as variâncias da variável independente, no caso simples, ou as matrizes de covariâncias das variáveis independentes, no caso múltiplo, para as \(C\) classes são distintas. A Figura 14.6 plota densidades bivariadas de dados de um caso de classificação binária com distintas variâncias entre classes.

Figura 14.6: Densidades teóricas de duas classes em função de duas variáveis para matrizes de covariâncias distintas

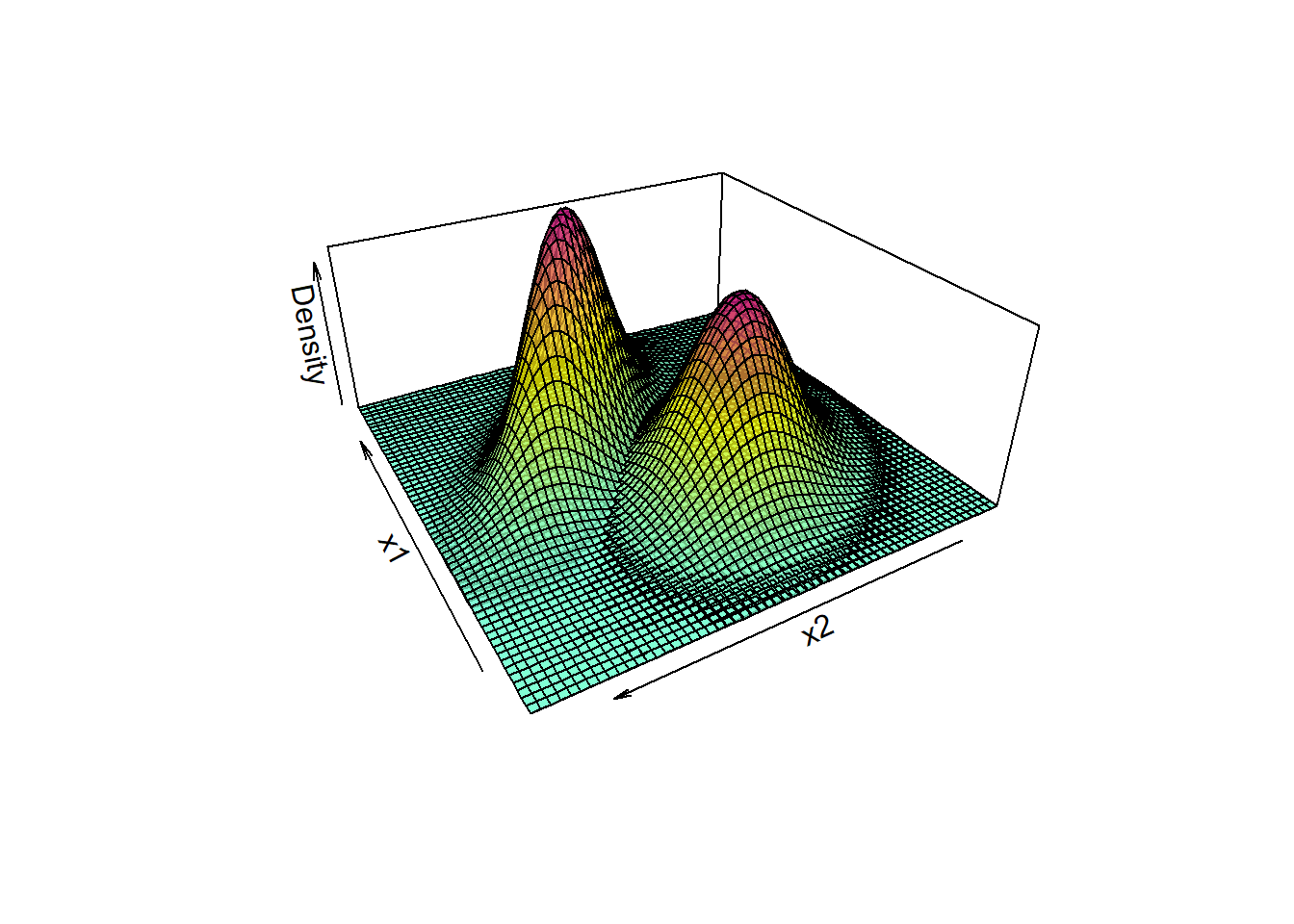
A fronteira de classificação em tais casos não será linear, conforme ilustrado na Figura 14.7.

Figura 14.7: Fronteira de discriminação binária para caso em função de duas variáveis considerando matrizes de covariâncias distintas

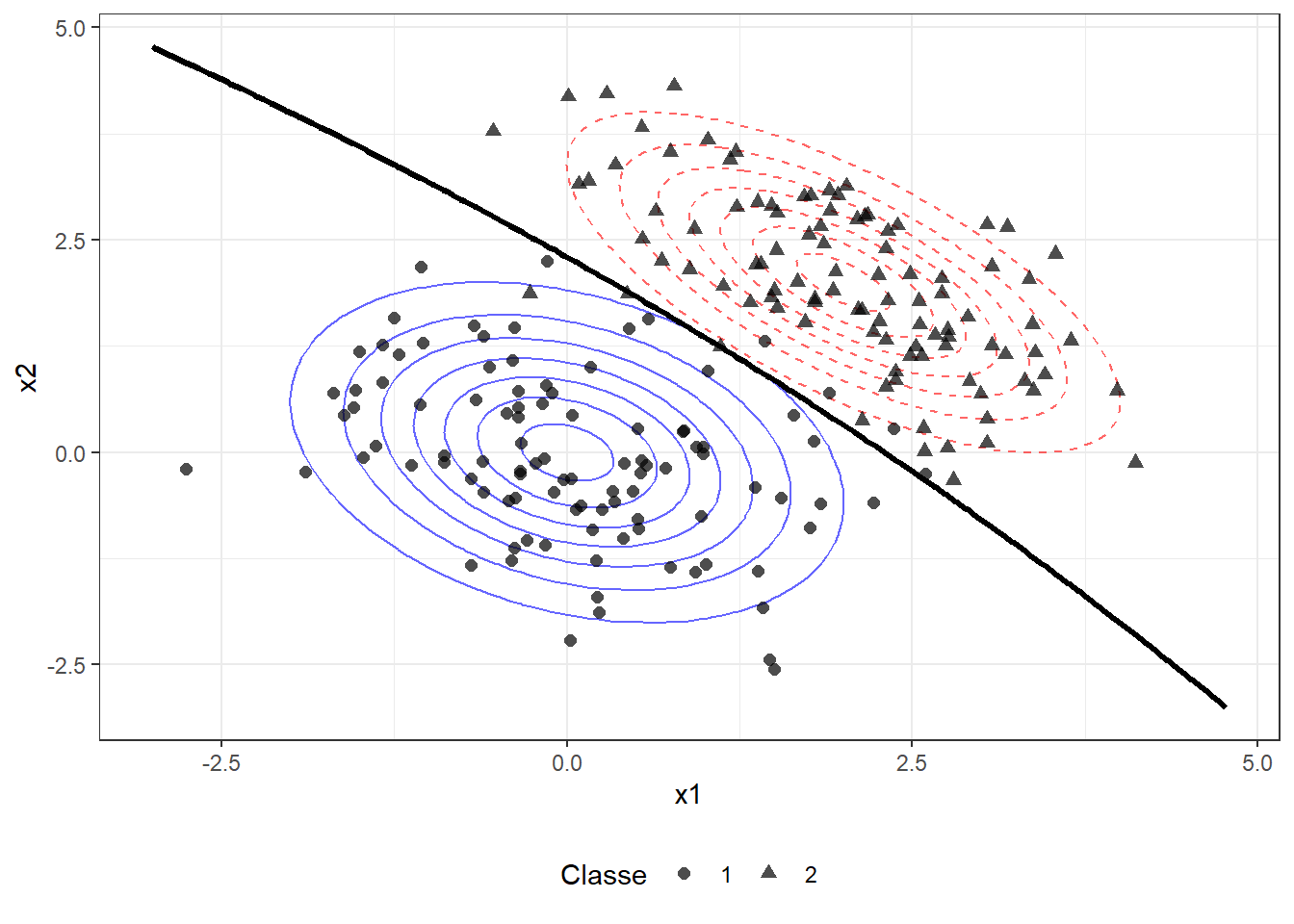
A função discriminante quadrática para a \(c\)-ésima classe pode ser escrita conforme Equação 14.17. Pode-se observar que neste caso não se desconsideram termos dependentes da matriz de covariância, uma vez que esta é diferente para cada classe. Deve-se calcular o valor de \(u_c\), \(c=1,\dots,C\), de forma a decidir sobre a classe com maior probabilidade.

\[ u_c(\mathbf x) = -\frac 1 2 (\mathbf x - \mu_c)^T \Sigma_c^{-1}(\mathbf x - \mu_c)-\frac 1 2 \text{log }(\Sigma_c) \tag{14.17}\]

Seja um conjunto de dados de medições de características de folhas de distintas espécies de árvores frutíferas encontradas no Brasil. A Tabela 14.2 expõe as primeiras observações do conjunto de dados.

Tabela 14.2: Observações do conjunto de dados folhas

especie	area	perimetro	raiomedio	raiosd	raiomin	raiomax	eixomaior	ecentricidade
goiaba	2.3587161	5.575758	0.9105212	0.1573576	0.6948606	1.1568970	2.313212	789
goiaba	2.2907601	5.818182	0.9124121	0.1605576	0.6507515	1.2462788	2.232667	763
goiaba	1.8871878	5.103030	0.8239879	0.1680606	0.5723879	1.1024121	2.146024	819
goiaba	1.2324738	5.224242	0.7478909	0.2848121	0.2493576	1.2367152	2.335758	941
goiaba	0.9707225	3.684848	0.6013455	0.1543394	0.3110061	0.8603394	1.675248	868
goiaba	2.1489390	6.072727	0.9169333	0.2829576	0.4715758	1.4316727	2.711770	909

A Figura 14.8 exibe gráficos de dispersão e correlações aos pares bem como densidades amostrais dentro de cada espécie considerada no conjunto de dados folha. Pode-se constatar que, dado a variação nas densidades amostrais para cada espécie nas distintas variáveis, a análise quadrática discriminante talvez seja mais adequada ao problema de clssificação em questão.

Figura 14.8: Diagramas de dispersão e correlações aos pares para o conjunto de dados folhas

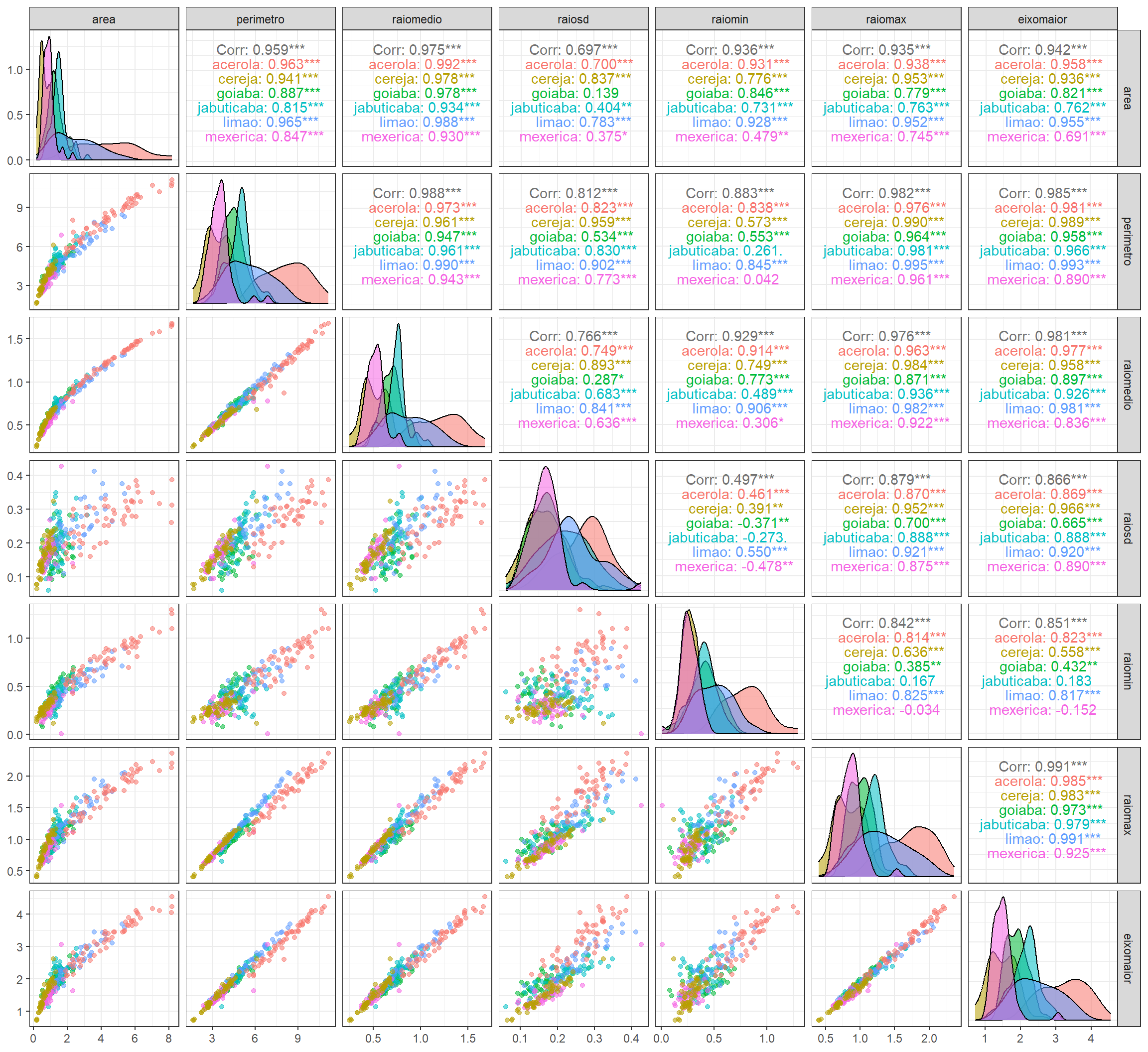
Tomando aleatoriamente 75% das observações para treino, um modelo obtido via QDA é obtido conforme segue.

Call:
qda(especie ~ ., data = data.treino2)

Prior probabilities of groups:
   acerola     cereja     goiaba jabuticaba      limao   mexerica 
 0.2291667  0.1666667  0.1666667  0.1527778  0.1458333  0.1388889 

Group means:
                area perimetro raiomedio    raiosd   raiomin   raiomax
acerola    4.6199258  8.300373 1.2320808 0.2681082 0.8241248 1.7416843
cereja     0.5802029  3.094874 0.4704354 0.1517791 0.2589256 0.7737258
goiaba     1.2797672  4.347291 0.6925562 0.1658400 0.4252010 0.9866172
jabuticaba 1.6047352  4.922163 0.7575936 0.2188675 0.4270077 1.1733904
limao      2.4424181  5.434424 0.8563618 0.2373312 0.5054323 1.3197574
mexerica   0.9791802  3.597199 0.5411255 0.1668078 0.2871625 0.8697244
           eixomaior ecentricidade
acerola     3.261431      835.0303
cereja      1.360406      907.8750
goiaba      1.883029      848.2500
jabuticaba  2.159333      879.9091
limao       2.436449      881.6667
mexerica    1.495607      869.9500

Tal modelo apresentou 88,89% de acuracidade. Sugere-se comparar o desempenho com o da análise discriminante linear.

            pred
y            acerola cereja goiaba jabuticaba limao mexerica
  acerola         19      0      0          0     0        0
  cereja           1     20      2          2     5        0
  goiaba           0      0     18          3     3        0
  jabuticaba       0      0      1         20     4        1
  limao            1      1      0          3    17        0
  mexerica         1      0      0          0     2       19

[1] 0.7902098

14.5 Implementações em R

A seguir serão expostas as implementações necessárias para obter os resultados do capítulo.

14.5.1 Análise linear discriminante

Carregando pacotes.

library(datasets)
library(dplyr)
library(GGally)
library(ggplot2)
theme_set(theme_bw())
library(MASS)
library(TreeDiagram)

Conjunto de dados iris.

data <- iris
head(iris)

Visualizando correlações e distribuição dentro das classes.

ggpairs(data, 
        aes(col=Species, alpha=.5), 
        progress=F) + 
  theme_bw()

Separando dados de treino e teste.

set.seed(1)

tr <- round(0.75*nrow(data))
treino <- sample(nrow(data), tr, replace = F)

data.treino <- data[treino,]
data.teste <- data[-treino,]

Análise linear discriminante.

fit.lda1 <- lda(Species ~ ., data.treino)
fit.lda1

Matriz de confusão para dados de teste.

lda.pred1 <- predict(fit.lda1, newdata=data.teste)

cm1 <- table(y=data.teste$Species, pred=lda.pred1$class)
cm1

14.5.2 Análise discriminante quadrática

Leitura de dados.

data2 <- read.csv("folhas.csv", header=T)
head(data2) |> gt()

Visualizando correlações e distribuição dentro das classes.

ggpairs(data2, aes(col=especie, alpha=.5), progress=F) + theme_bw()

Separando dados de treino e teste.

set.seed(1)

tr2 <- round(0.75*nrow(data2))
treino2 <- sample(nrow(data2), tr2, replace = F)

data.treino2 <- data2[treino2,]
data.teste2 <- data2[-treino2,]

Modelagem via LDA.

fit.lda2 <- lda(especie ~ ., data.treino2)
fit.lda2

Desempenho de teste.

lda.pred2 <- predict(fit.lda2, newdata=data.teste2)

cm2 <- table(y=data.teste2$especie, pred=lda.pred2$class)
cm2

sum(diag(cm2))/sum(cm2)

Modelagem via QDA.

fit.qda2 <- qda(especie ~ ., data.treino2)
fit.qda2

Desempenho de teste.

qda.pred2 <- predict(fit.qda2, newdata=data.teste2)

cm3 <- table(y=data.teste2$especie, pred=qda.pred2$class)
cm3

sum(diag(cm3))/sum(cm3)