| x1 | x2 | y |
|---|---|---|
| -0.08 | 1.24 | 2.34 |
| 0.84 | 2.29 | 2.76 |
| -0.46 | 2.42 | 2.34 |
| -0.55 | 0.71 | 1.68 |
| 0.74 | 2.07 | 3.01 |
| -0.11 | 1.19 | 1.84 |
| -0.17 | 3.51 | 2.61 |
| -1.09 | 1.73 | 2.38 |
| -3.01 | 3.56 | 2.10 |
| -0.59 | 1.76 | 1.75 |
8 Regressão por máquinas de reforço de gradiente
8.1 Máquinas de reforço de gradiente
As máquinas de reforço de gradiente (gradient boosting machines - GBM) foram propostas por Gerome Friedman e consistem em um método de aprendizado por reforço que visa aproximar o gradiente da função perda, ou de forma mais simples, visa aproximar o erro de previsão e diminuir este a cada iteração do método. O conceito de aprendizado por reforço está relacionado ao fato de o método de certa forma aprender através do erro, uma vez que vai melhorando a previsão a cada tentativa ou iteração a partir dos valores residuais ou de erro observados. O gradiente ou erro é gradativamente reduzido aproximando-o de forma iterativa considerando uma taxa de aprendizagem. O método foi proposto inicialmente considerando árvores de decisão ou regressão, mas poderia ser utilizado também no caso de regressão por mínimos quadrados.
Um algoritmo GBM simplista do método GBM para regressão é apresentado à seguir:
- Defina \(\hat{f}(\mathbf{x})=0\) e \(\varepsilon_i = y_i\) para todos dados de treino.
- Para \(m=1,...,M\):
- Estime uma árvore, \(\hat{f}_m\), para os dados de treino \((\mathbf{x}_i,\varepsilon_i)\), \(i=1,...,N\);
- Atualize \(\hat{f}(\mathbf{x})\) adicionando a árvore de regressão obtida multiplicada por uma taxa de aprendizagem \(\lambda\), isto é, \(\hat{f}(\mathbf{x}) \leftarrow \hat{f}(\mathbf{x}) + \lambda\hat{f}_m(\mathbf{x})\);
- Atualize os resíduos, isto é \(\varepsilon_i \leftarrow \varepsilon_i - \lambda\hat{f}_m(\mathbf{x}_i)\), \(i=1,...,N\);
- Atualize o modelo “impulsionado” ou “reforçado”: \(\hat{f}(\mathbf{x}) = \sum_{m=1}^M\lambda\hat{f}_m(\mathbf{x})\)
O número de iterações ou árvores consideradas, \(M\), pode ser definido por validação cruzada. A taxa de aprendizado, \(\lambda\), geralmente é um valor real muito pequeno, por exemplo 0,01 ou 0,001 e define a taxa que o modelo por refroço aprende, isto é, melhora sua previsão. Quanto menor \(\lambda\), maior o número de árvores, \(M\), necessário para uma boa aproximação.
Geralmente \(\hat{f}_m(\mathbf{x})\) é um modelo de árvore com apenas uma partição e portanto dois nós terminais ou regiões, sendo portanto um aprendiz fraco (weak leaner). Em alguns casos pode ser interessante modelos com árvores com duas partições, o que de certa forma implica em modelos com interação.
Considerando a função perda quadrática comumente usada em problemas de regressão:
\[ \begin{aligned} L = \frac{1}{2}(y - \hat{f}(\mathbf{x}))^2 \end{aligned} \]
A divisão por 2 viabiliza facilitar os cálculos no algoritmo de boosting. Tomando a derivada de \(L\) em relação a \(f\) obtém-se o valor residual ou erro em relação à resposta de interesse, conforme Equação 8.1.
\[ \begin{aligned} \frac{\partial L}{\partial f} = y - \hat{f}(\mathbf{x}) = \varepsilon \end{aligned} \tag{8.1}\]
Portanto, em cada iteração, o algoritmo GBM, ao aproximar uma árvore considerando \(N\) observações das variáveis regressoras, \(\mathbf{x}_i\), em relação à \(N\) valores residuais, \(\varepsilon_i\), \(i=1,...,N\), aproxima o gradiente da função perda que, no caso da função perda quadrática, é o valor residual ou erro, \(\varepsilon\).
8.1.1 Implementação simplista passo a passo do GBM para regressão
Para entender melhor o algoritmo GBM, considere o conjunto arbitrário de dados de treino da Tabela 8.1, com duas variáveis independentes, \(x_1\) e \(x_2\), e uma dependente contínua, \(y\).
Consideremos para fins didáticos uma taxa de aprendizagem alta, \(\lambda\) = 0,5, e um número pequeno de iterações, \(M = 4\) árvores. O algoritmo inicia fazendo \(\hat{f}(x_1,x_2)=0\) e \(\varepsilon_i = y_i\), isto é (a penúltima coluna seriam os valores previstos do modelo inicial, \(\hat{f} = f\), e a última coluna seria o erro, \(\varepsilon = e\)), conforme Tabela 8.2.
| x1 | x2 | y | f | e |
|---|---|---|---|---|
| -0.08 | 1.24 | 2.34 | 0 | 2.34 |
| 0.84 | 2.29 | 2.76 | 0 | 2.76 |
| -0.46 | 2.42 | 2.34 | 0 | 2.34 |
| -0.55 | 0.71 | 1.68 | 0 | 1.68 |
| 0.74 | 2.07 | 3.01 | 0 | 3.01 |
| -0.11 | 1.19 | 1.84 | 0 | 1.84 |
| -0.17 | 3.51 | 2.61 | 0 | 2.61 |
| -1.09 | 1.73 | 2.38 | 0 | 2.38 |
| -3.01 | 3.56 | 2.10 | 0 | 2.10 |
| -0.59 | 1.76 | 1.75 | 0 | 1.75 |
Fazendo \(m=1\), estima-se a primeira árvore, \(\hat{f} = T\), para os resíduos em função das variáveis independentes, \((x_1,x_2,\varepsilon)_i\), \(i=1,...,N\), conforme segue.
node), split, n, deviance, yval
* denotes terminal node
1) root 10 1.7560 2.281
2) x2 < 1.915 5 0.4505 1.998 *
3) x2 > 1.915 5 0.5049 2.564 *O modelo obtido é usado para atualizar os valores previstos, \(\hat{f}(x_1,x_2)\leftarrow \hat{f}(x_1,x_2) + \lambda\hat{f}_1(x_1,x_2)\) e os resíduos, \(\varepsilon_i \leftarrow \varepsilon_i - \lambda\hat{f}_1(x_1,x_2)\), conforme Tabela 8.3.
| x1 | x2 | y | f | e |
|---|---|---|---|---|
| -0.08 | 1.24 | 2.34 | 0.999 | 1.341 |
| 0.84 | 2.29 | 2.76 | 1.282 | 1.478 |
| -0.46 | 2.42 | 2.34 | 1.282 | 1.058 |
| -0.55 | 0.71 | 1.68 | 0.999 | 0.681 |
| 0.74 | 2.07 | 3.01 | 1.282 | 1.728 |
| -0.11 | 1.19 | 1.84 | 0.999 | 0.841 |
| -0.17 | 3.51 | 2.61 | 1.282 | 1.328 |
| -1.09 | 1.73 | 2.38 | 0.999 | 1.381 |
| -3.01 | 3.56 | 2.10 | 1.282 | 0.818 |
| -0.59 | 1.76 | 1.75 | 0.999 | 0.751 |
Tomando \(m=2\), repete-se o processo, obtendo-se uma nova árvore para os resíduos e atualizando as previsões e os resíduos, conforme Tabela 8.4.
node), split, n, deviance, yval
* denotes terminal node
1) root 10 1.1560 1.1400
2) x1 < -0.315 5 0.3261 0.9378 *
3) x1 > -0.315 5 0.4187 1.3430 *| x1 | x2 | y | f | e |
|---|---|---|---|---|
| -0.08 | 1.24 | 2.34 | 1.6706 | 0.6694 |
| 0.84 | 2.29 | 2.76 | 1.9536 | 0.8064 |
| -0.46 | 2.42 | 2.34 | 1.7509 | 0.5891 |
| -0.55 | 0.71 | 1.68 | 1.4679 | 0.2121 |
| 0.74 | 2.07 | 3.01 | 1.9536 | 1.0564 |
| -0.11 | 1.19 | 1.84 | 1.6706 | 0.1694 |
| -0.17 | 3.51 | 2.61 | 1.9536 | 0.6564 |
| -1.09 | 1.73 | 2.38 | 1.4679 | 0.9121 |
| -3.01 | 3.56 | 2.10 | 1.7509 | 0.3491 |
| -0.59 | 1.76 | 1.75 | 1.4679 | 0.2821 |
Para \(m=3\), tem-se os resultados resumidos na Tabela 8.5.
node), split, n, deviance, yval
* denotes terminal node
1) root 10 0.8475 0.5702
2) x2 < 1.915 5 0.4252 0.4490 *
3) x2 > 1.915 5 0.2753 0.6915 *| x1 | x2 | y | f | e |
|---|---|---|---|---|
| -0.08 | 1.24 | 2.34 | 1.89511 | 0.44489 |
| 0.84 | 2.29 | 2.76 | 2.29934 | 0.46066 |
| -0.46 | 2.42 | 2.34 | 2.09664 | 0.24336 |
| -0.55 | 0.71 | 1.68 | 1.69241 | -0.01241 |
| 0.74 | 2.07 | 3.01 | 2.29934 | 0.71066 |
| -0.11 | 1.19 | 1.84 | 1.89511 | -0.05511 |
| -0.17 | 3.51 | 2.61 | 2.29934 | 0.31066 |
| -1.09 | 1.73 | 2.38 | 1.69241 | 0.68759 |
| -3.01 | 3.56 | 2.10 | 2.09664 | 0.00336 |
| -0.59 | 1.76 | 1.75 | 1.69241 | 0.05759 |
Finalmente, para \(m=4\), obtém-se o modelo “reforçado” final que consiste na soma ponderada pela taxa de aprendizagem de todos os modelos, isto é, \(\hat{f}(\mathbf{x}) = \sum_{m=1}^M\lambda\hat{f}_m(\mathbf{x})\), com resultados resumidos na Tabela 8.6.
node), split, n, deviance, yval
* denotes terminal node
1) root 10 0.7372 0.2851
2) x1 < -0.315 5 0.3436 0.1959 *
3) x1 > -0.315 5 0.3140 0.3744 *| x1 | x2 | y | f | e |
|---|---|---|---|---|
| -0.08 | 1.24 | 2.34 | 2.082286 | 0.257714 |
| 0.84 | 2.29 | 2.76 | 2.486516 | 0.273484 |
| -0.46 | 2.42 | 2.34 | 2.194589 | 0.145411 |
| -0.55 | 0.71 | 1.68 | 1.790359 | -0.110359 |
| 0.74 | 2.07 | 3.01 | 2.486516 | 0.523484 |
| -0.11 | 1.19 | 1.84 | 2.082286 | -0.242286 |
| -0.17 | 3.51 | 2.61 | 2.486516 | 0.123484 |
| -1.09 | 1.73 | 2.38 | 1.790359 | 0.589641 |
| -3.01 | 3.56 | 2.10 | 2.194589 | -0.094589 |
| -0.59 | 1.76 | 1.75 | 1.790359 | -0.040359 |
Obviamente, o processo poderia seguir para melhorar as previsões. Conforme já elucidado, pode-se definir o número de iterações por validação cruzada. Quanto maior o número de árvores estipulado, recomenda-se que menor seja a taxa de aprendizagem.
Seja um conjunto de dados para prever o rendimento de indivíduos considerando anos de experiência, ocupação, se ele trabalha ou não na indústria, escolaridade, além de fatores sócio-geográficos. Considerando um modelo obtido via GBM com 8000 árvores e \(\lambda = 0,1\), pode-se plotar um gráfico de superfície considerando como variáveis independentes a escolaridade e anos de experiência conforme Figura 8.1.
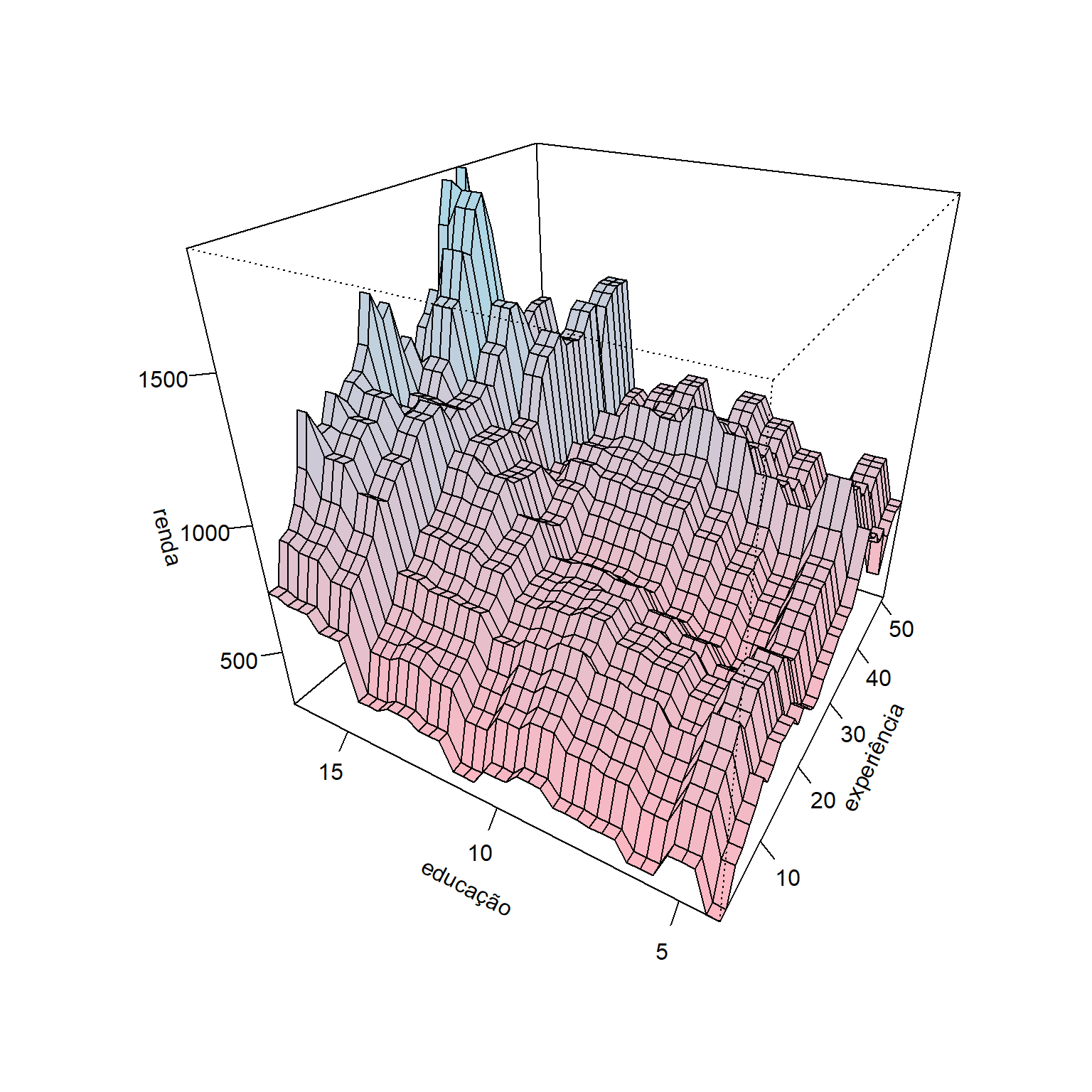
8.2 Implementações em R
A seguir serão expostas as implementações necessárias para obter os resultados do capítulo.
8.2.1 GBM para regressão passo a passo
Carregando pacotes.
library(AER)
library(gbm)
library(tree)
library(GGally)
library(modelsummary)
library(tidyverse)
library(kernlab)Entendendo as máquinas de reforço de gradiente com um exemplo arbitrário com 10 observações de treino, duas variáveis independentes, \(x_1\) e \(x_2\), e uma dependente contínua, \(y\).
set.seed(8)
x1 <- rnorm(10)
x2 <- rnorm(10, 2)
y <- 0.3*x1+sqrt(x2)+rnorm(10,1,0.2)
dat <- round(data.frame(x1,x2,y),2)
datSeja a taxa de aprendizagem \(\lambda\) = 0.5 e \(M = 4\) árvores ou iterações. A previsão inicial é nula e os resíduos recebem os valores observados da resposta:
dat$f <- 0
dat$e <- dat$y
lambda <- 0.5
datEstimanado a primeira árvore para os resíduos.
tree1 <- tree(e ~ x1+x2, dat)
tree1Atualizando os valores previstos e os resíduos.
pred1 <- predict(tree1, dat)
dat$f <- dat$f + lambda*pred1
dat$e <- dat$e -lambda*pred1
datNa segunda iteração, repete-se o processo, obtendo-se uma nova árvore para os resíduos e atualizando as previsões e os resíduos. Pode-se constatar que a cada iteração vamos melhorando os valores previstos e, portanto, diminuindo os valores residuais.
tree2 <- tree(e ~ x1+x2, dat)
tree2pred2 <- predict(tree2, dat)
dat$f <- dat$f + lambda*pred2
dat$e <- dat$e -lambda*pred2
datNa terceira iteração, tem-se:
tree3 <- tree(e ~ x1+x2, dat)
tree3pred3 <- predict(tree3, dat)
dat$f <- dat$f + lambda*pred3
dat$e <- dat$e -lambda*pred3
datFinalmente, na quara e última iteração, obtém-se o modelo “reforçado” final que consiste na soma ponderada pela taxa de aprendizagem de todos os modelos.
tree4 <- tree(e ~ x1+x2, dat)
tree4pred4 <- predict(tree4, dat)
dat$f <- dat$f + lambda*pred4
dat$e <- dat$e -lambda*pred4
dat8.2.2 Previsão do rendimento em função da escolaridade, experiência e outras variáveis sócio-geográficas
Seja um conjunto de dados para prever o rendimento de indivíduos considerando anos de experiência, ocupação, se ele trabalha ou não na indústria, escolaridade, além de fatores sócio-geográficos.
data(PSID7682)
# ?PSID7682
dados <- PSID7682
dados <- dados[,-c(13:14)]
library(modelsummary)
datasummary_skim(dados)| Unique | Missing Pct. | Mean | SD | Min | Median | Max | Histogram | |
|---|---|---|---|---|---|---|---|---|
| experience | 51 | 0 | 19.9 | 11.0 | 1.0 | 18.0 | 51.0 |  |
| weeks | 41 | 0 | 46.8 | 5.1 | 5.0 | 48.0 | 52.0 |  |
| education | 14 | 0 | 12.8 | 2.8 | 4.0 | 12.0 | 17.0 |  |
| wage | 1017 | 0 | 882.9 | 442.8 | 100.0 | 800.0 | 5100.0 |  |
| N | % | |||||||
| occupation | white | 2036 | 48.9 | |||||
| blue | 2129 | 51.1 | ||||||
| industry | no | 2518 | 60.5 | |||||
| yes | 1647 | 39.5 | ||||||
| south | no | 2956 | 71.0 | |||||
| yes | 1209 | 29.0 | ||||||
| smsa | no | 1442 | 34.6 | |||||
| yes | 2723 | 65.4 | ||||||
| married | no | 773 | 18.6 | |||||
| yes | 3392 | 81.4 | ||||||
| gender | male | 3696 | 88.7 | |||||
| female | 469 | 11.3 | ||||||
| union | no | 2649 | 63.6 | |||||
| yes | 1516 | 36.4 | ||||||
| ethnicity | other | 3864 | 92.8 | |||||
| afam | 301 | 7.2 |
Separando metade das observações para treino do modelo.
set.seed(78)
tr <- round(0.5*nrow(dados))
treino <- sample(nrow(dados), tr, replace = F)Obtendo um modelo via GBM com 10000 árvores e \(\lambda = 0,1\).
boost1 <- gbm(log(wage)~., data = dados, distribution = "gaussian",
n.trees = 10000, bag.fraction = 0.7,
interaction.depth = 2, shrinkage = 0.1)
summary(boost1)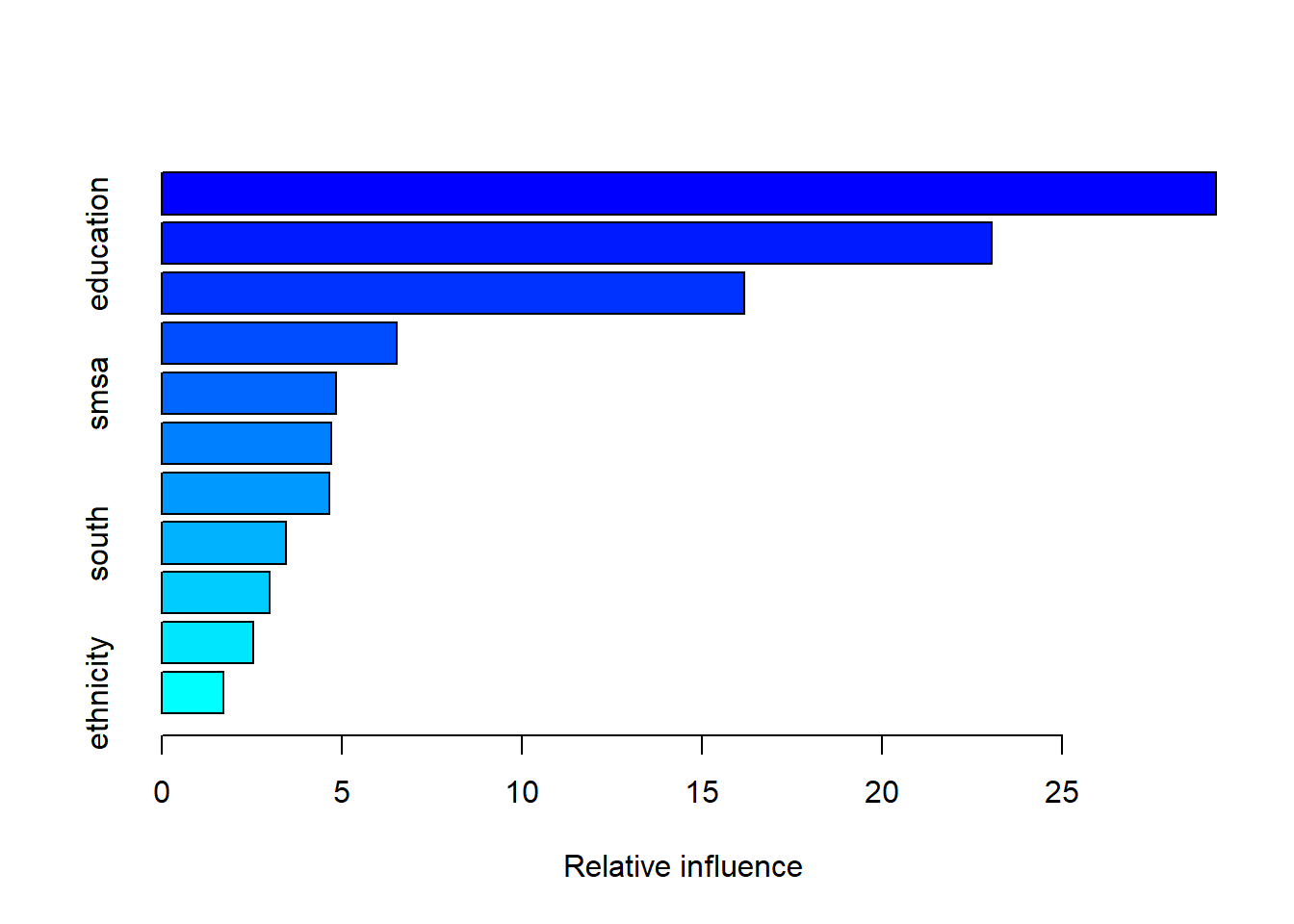
var rel.inf
experience experience 29.285767
education education 23.061164
weeks weeks 16.194209
gender gender 6.516940
smsa smsa 4.849954
occupation occupation 4.713714
union union 4.660501
south south 3.456731
industry industry 3.010622
married married 2.534908
ethnicity ethnicity 1.715492metrics <- function(obs, pred) {
RSE <- sum((obs - pred)^2)
SST <- sum((obs - mean(obs))^2)
R2 <- 1 - RSE/SST
MAE <- mean(abs(obs - pred))
RMSE <- sqrt(mean((obs - pred)^2))
return(
data.frame(RMSE = RMSE,
MAE = MAE,
R2 = R2))
}Desempenho de treino.
pred <- predict(boost1, dados[treino,])Using 10000 trees...metrics(log(dados$wage[treino]),pred) RMSE MAE R2
1 0.2803965 0.2171146 0.6402183Testando o modelo.
pred1 <- predict(boost1, dados[-treino,])Using 10000 trees...metrics(log(dados$wage[-treino]),pred1) RMSE MAE R2
1 0.2752103 0.2104087 0.6347375Referências
Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.
Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An introduction to statistical learning: with applications in R. Spinger.