11 Redes neurais para regressão

Autor

Robson Bruno Dutra Pereira

11.1 Definições iniciais

Seja um vetor de \(K\) variáveis regressoras \(\mathbf{x}=[x_1,x_2,\ldots,x_K]^T\), uma variável dependente ou de resposta contínua, \(y \in \mathbf{R}\) e \(N\) observações de treino disponíveis, \(\{x_1,y_1\}, \{x_2,y_2\}, \ldots, \{x_N,y_N\}\).

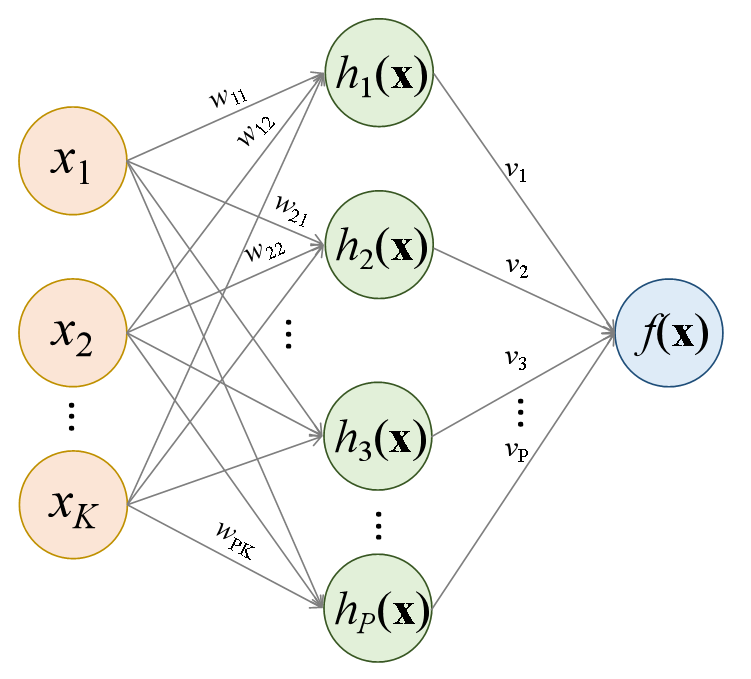
Uma rede neural com 1 camada oculta é ilustrada na Figura 11.1. Esta rede apresenta \(K\) variáveis preditoras ou independentes na camada de entrada, \(P\) neurônios na camada oculta, \(h_1(\mathbf{x})\), \(h_2(\mathbf{x})\), …, \(h_P(\mathbf{x})\), e entrega na camada de saída o modelo \(f(\mathbf{x})\).

Figura 11.1: Rede neural com uma camada oculta

Começando de trás para frente, o modelo final pode ser definido a partir da Equação 11.1. \[ \begin{matrix} f(\mathbf{x})=v_0 + v_1h_1(\mathbf{x}) + v_2h_2(\mathbf{x}) + \ldots + v_Ph_P(\mathbf{x}) \\ f(\mathbf{x})=v_0 + \sum_{p=1}^Pv_ph_p(\mathbf{x}) = \mathbf{v}^T\mathbf{h} \end{matrix} \tag{11.1}\]

onde \(\mathbf{v} = [v_0, v_1, ..., v_P]^T\) é um vetor de pesos do modelo final na camada oculta e \(\mathbf{h} = [1, h_1(\mathbf{x}), ... h_P(\mathbf{x})]^T\) é um vetor de funções computadas na camada oculta. O \(p\)-ésimo termo \(h_p(\mathbf{x})\), \(p=1, ..., P\), da camada oculta é calculado conforme Equação 11.2. \[ \begin{matrix} h_p=g(w_{p0} + w_{p1}x_1 + w_{p2}x_2 + \ldots + w_{pK}x_K) \\ h_p=g(w_{p0} + \sum_{k=1}^Kw_{pk}x_k) = g(\mathbf{w}_p^T\mathbf{x})\\ \end{matrix} \tag{11.2}\]

onde \(\mathbf{w}_p = [w_{p0}, w_{p1}, \ldots, w_{pK}]^T\) é um vetor de pesos do \(p\)-ésimo neurônio na camada de entrada e \(g(z)\) é uma função de ativação a qual deve ser selecionada de forma apropriada ao tipo de problema abordado. É importante observar que tano na camada oculta quanto na camada de saída não foram ilustrados na Figura 11.1 os termos de vício \(v_0\) e \(w_{0p}\), porém são importantes e considerados no modelo. Para problemas de regressão a função de unidade linear retificada (Retified Linear Unit - ReLU) pode ser usada como ativação nas camadas ocultas, sendo esta descrita matematicamente conforme Equação 11.3.

\[ g(z) = max(0,z) = \bigg\{ \begin{matrix} 0,z<0 \\ z,z\geq0 \end{matrix} \tag{11.3}\]

A função de ativação ReLu é plotada a seguir. Uma vez que no processo de otimização dos parâmetros da rede, o gradiente da função perda em relação a tais parâmetros é computado iterativamente, a função de ativação ReLU apresenta a vantagem de ter derivada nula para valores negativos de \(z\), desativando alguns neurônios quando \(z \leq 0\), tornando os cálculos computacionais mais fáceis.

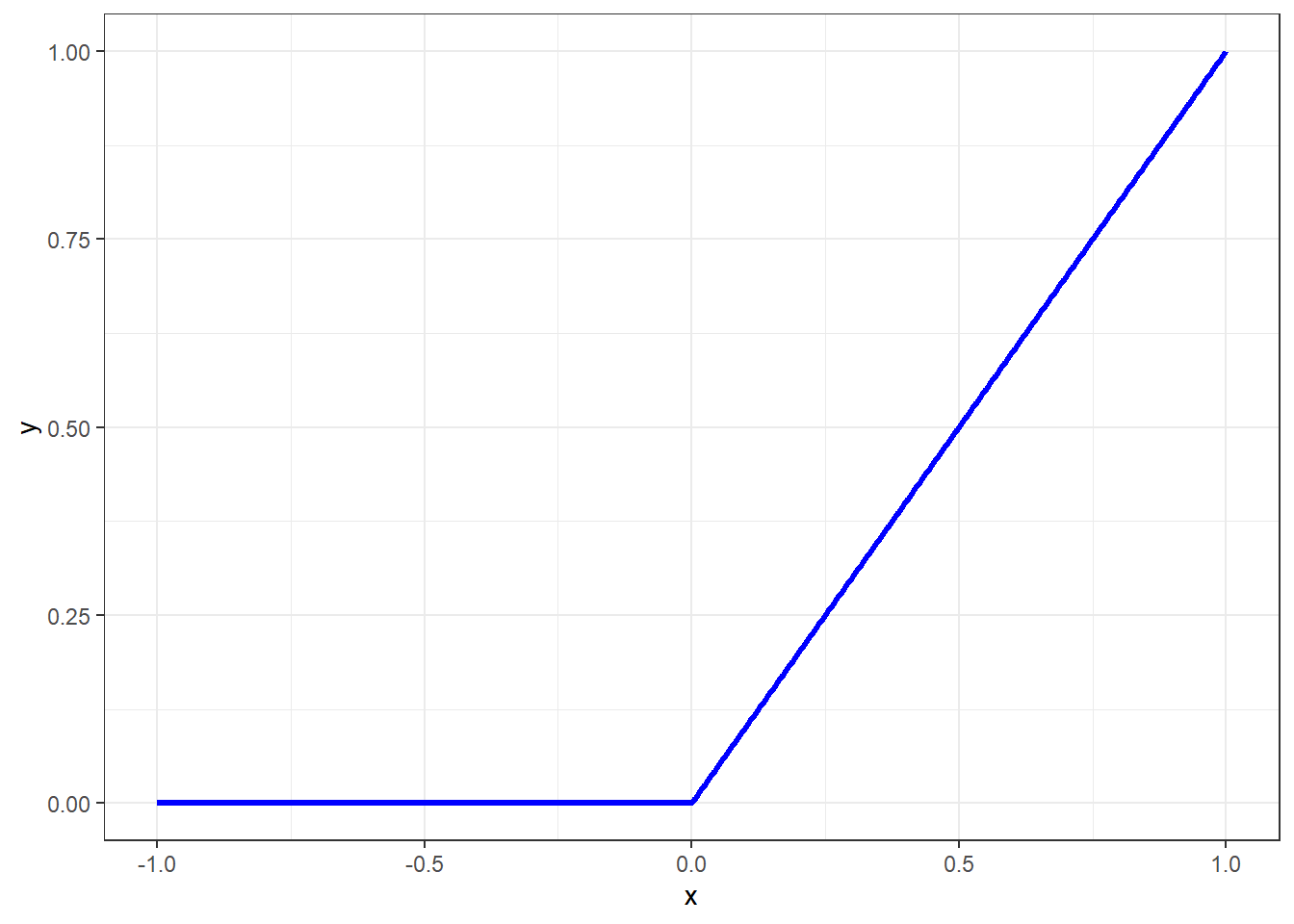
É importante esclarecer que a função ReLU deve ser utilizada em camadas ocultas, conforme a descrição matemática aqui sugere. Ademais em problemas de regressão não se usa uma função de ativação na camada de saída, ainda de acordo com a formulação aqui exposta. Oportunamente, quando o tema classificação for abordado, outras funções de ativação serão expostas, além de adaptações necessárias.

Dadas tais considerações, pode-se escrever o modelo explícito para uma rede neural com uma camada oculta conforme segue. \[ \begin{aligned} f(\mathbf{x})=v_0 + v_1.g(w_{10} + w_{11}x_1 + w_{12}x_2 + \ldots + w_{1K}x_K)\\ + v_2.g(w_{20} + w_{21}x_1 + w_{22}x_2 + \ldots + w_{2K}x_K)\\ + \ldots + v_P.g(w_{P0} + w_{P1}x_1 + w_{P2}x_2 + \ldots + w_{PK}x_K) \end{aligned} \]

Logo, \[ \begin{matrix} f(\mathbf{x})=v_0 + v_1.g(w_{10} + \sum_{k=1}^Kw_{1k}x_k) + v_2.g(w_{20} + \sum_{k=1}^Kw_{2k}x_k) + \ldots \\ + v_P.g(w_{P0} + \sum_{k=1}^Kw_{Pk}x_k) \end{matrix} \]

De forma, mais compacta, temos o modelo já exposto anteriormente. \[ \begin{matrix} f(\mathbf{x})=v_0 + \sum_{p=1}^Pv_p.g(w_{p0} + \sum_{k=1}^Kw_{pk}x_k)\\ f(\mathbf{x})=v_0 + \sum_{p=1}^Pv_ph_p(\mathbf{x}) = \mathbf{v}^T\mathbf{h}\\ \end{matrix} \]

O aprendizado profundo consiste simplesmente em uma rede neural com duas ou mais camadas ocultas.

11.2 Descida do gradiente e propagação para trás

Os parâmetros a serem estimados do modelo de rede neural consistem em \(\mathbf{v} = [v_0, v_1,v_2,\ldots,v_p]^T\) e \(\mathbf{w}_p=[w_{p0},w_{p1},w_{p2},\ldots,w_{pK}]^T\). Tomando as \(N\) observações de treino \((\mathbf{x}_i,y_i)\), \(i=1,...,N\), estima-se o modelo minimizando a função perda quadrática da Equação 11.4. \[ \min_{\{w_p\}_1^N,v} \frac{1}{2} \sum_{i=1}^{N}(y_i-f(\mathbf{x}_i))^2 \tag{11.4}\]

onde

\[ f(\mathbf{x})=v_0+\sum_{p=1}^Pv_p.g(w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik}). \]

Devido a não convexidade da função perda, múltiplas soluções podem estar presentes. A otimização é realizada de forma lenta e iterativa com o algoritmo de descida do gradiente. Seja \(\mathbf{\theta}\) o vetor de todos os parâmetros da rede, \(\mathbf{\theta} = [\mathbf{v}, \mathbf{w}_0, \mathbf{w}_1, ..., \mathbf{w}_P]^T\). A fução perda pode ser reescrita conforme Equação 11.5. \[ L(\theta)=\frac{1}{2} \sum_{i=1}^{N}(y_i-f_\theta(\mathbf{x}_i))^2 \tag{11.5}\]

O algoritmo de descida do gradiente pode ser descrito a partir dos seguintes passos:

Defina um valor inicial \(\theta_0\) para \(\theta\).
Itere até \(L(\theta)\) parar de decrescer ou então até um critério de parada:

Encontre um vetor \(\delta\) de forma que \(\theta_{t+1}=\theta_t+\delta\) reduza \(L(\theta)\).
Faça \(t \leftarrow t+1\).

O valor de \(\delta\) deve ser escolhido na direção de máximo crescimento da função perda. O algoritmo de propagação para trás (backpropagation) considera o gradiente da função perda em relação aos parâmetros da rede, isto é, \[ \nabla L(\theta_t)=\frac{\partial L}{\partial \theta} \Bigg|_{\theta=\theta_t}. \]

Como \(\nabla L(\theta_t)\), que consiste no vetor de derivadas parciais de \(L\) avaliadas em \(\theta_t\), o algoritmo de descida do gradiente busca mover o vetor \(\theta\) na direção contrária do gradiente, considerando uma taxa de aprendizagem \(\rho\) pequena para facilitar a convergência, isto é, \[ \theta_{t+1} \leftarrow \theta_t - \rho \nabla L(\theta_t) \]

A propagação para trás consiste simplesmente na aplicação da regra da cadeia de diferenciação. Como \[ L(\theta)=\sum_{i=1}^NL_i(\theta)=\frac{1}{2} \sum_{i=1}^{N}(y_i-f_\theta(\mathbf{x}_i))^2 \] é uma soma, o gradiente também será uma soma em \(N\). Assim, a derivada pode ser computada termo a termo, para cada observação \(i\): \[ L_i=\frac{1}{2} (y_i-v_0-\sum_{p=1}^Pv_p.g(w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik}))^2. \]

Considerando o termo \(v_p\), a derivada parcial da função perda pela regra da cadeia fica conforme segue:

\[ \frac{\partial L_i}{\partial v_p}=\frac{\partial L_i}{\partial f_\theta}\frac{\partial f_\theta}{\partial v_p} \]

\[ \frac{\partial L_i}{\partial v_p}=-(y_i-f_\theta(\mathbf{x}_i)).g(w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik}). \]

Já derivando em relação ao termo \(w_{pk}\), tem-se: \[ \frac{\partial L_i}{\partial w_{pk}}=\frac{\partial L_i}{\partial f_\theta}\frac{\partial f_\theta}{\partial g(w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik})}\frac{\partial g(w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik})}{\partial (w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik})} \frac{\partial (w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik})}{\partial w_{pk}} \]

\[ \frac{\partial L_i}{\partial w_{pk}}=-(y_i-f_\theta(\mathbf{x}_i))v_pg'(w_{p0}+\sum_{k=1}^Kw_{pk}x_{ik})x_{ik}. \]

Pode-se observar que em ambos resultados das derivadas os resíduos \(y_i-f_\theta(\mathbf{x}_i)\) estão presentes. Ou seja, na diferenciação uma fração do resíduos é atribuída aos parâmetros a partir da regra da cadeia.

Dada a possibilidade de overfitting no processo de otimização dos parâmetros da rede, diversas estratégias são usadas. Por exemplo a regularização ou penalização rígida ou LASSO pode ser aplicada, sendo a função perda modificada conforme Equação 11.6 para o primeiro caso. \[ L(\theta)=\frac{1}{2} \sum_{i=1}^{N}(y_i-f_\theta(\mathbf{x}))^2 +\lambda\sum_p\theta_p^2 \tag{11.6}\]

Outra estratégia utilizada é o dropout, que consiste na remoção aleatória de uma proporção dos neurônios de uma ou mais camadas. Este processo tem, de certa forma, similaridade com a estratégia de regularização via LASSO e também com a estratégia de seleção de variáveis para o particionamento binário recursivo no algoritmo de floresta aleatória.

O processo de treinamento da rede neural envolve a definição da arquitetura da rede, isto é, o número de camadas ocultas e o número de neurônios em cada uma, além da otimização dos hiperparâmetros de encolhimento e dropout. Todos estes podem ser considerados hiperpâmetros a serem otimizados e, para tal, deve-se utilizar de validação cruzada e grid search.

Existem diversos outros tipos de redes neurais, como as redes neurais convolucionais, com grande potencial para classificação de imagens e as redes neurais recorrentes, para problemas de séries temporais, reconhecimento de fala, entre outros. O leitor é convidado a ler a bibliografia citada para mais informações.

11.3 Implementação de uma rede neural para regressão passo a passo na linguagem R

A seguir será implementada uma rede neural com algoritmo de propagação para trás, passo a passo.

set.seed(123)

# Bibliotecas necessárias
library(ggplot2)
library(gridExtra)
theme_set(theme_bw())

Inicialmente define-se a função de ativação ReLU.

# Função ReLU: g(z) = max(0, z)
relu <- function(z) {
  result <- pmax(0, z)
  # Garantir que mantenha as dimensões originais
  if (is.matrix(z)) {
    result <- matrix(result, nrow = nrow(z), ncol = ncol(z))
  }
  return(result)
}

# Derivada da ReLU: g'(z) = 1 se z > 0, 0 caso contrário
relu_derivative <- function(z) {
  result <- as.numeric(z > 0)
  # Garantir que mantenha as dimensões originais
  if (is.matrix(z)) {
    result <- matrix(result, nrow = nrow(z), ncol = ncol(z))
  }
  return(result)
}

Em sequência são gerados dados fictícios para regressão, com duas variáveis independentes e a resposta.

# Gerar dados 
n <- 1000
x1 <- runif(n, -2, 2)
x2 <- runif(n, 0, 4)
noise <- rnorm(n, 0, 0.1)

# Função verdadeira: y = 0.3*x1 + sqrt(x2) + ruído
y_true <- 0.3 * x1 + sqrt(x2)
y <- y_true + noise

# Padronizar as variáveis para melhor convergência
x1_scaled <- scale(x1)[,1]
x2_scaled <- scale(x2)[,1]
y_scaled <- scale(y)[,1]

# Dividir em treino (80%) e teste (20%)
treino <- sample(1:n, 0.8 * n)
x1_train <- x1_scaled[treino]
x2_train <- x2_scaled[treino]
y_train <- y_scaled[treino]

x1_test <- x1_scaled[-treino]
x2_test <- x2_scaled[-treino]
y_test <- y_scaled[-treino]

A rede neural e o algortmo de propagação para trás e treinamento são implementados à seguir. Inicialmente defini-se a função da rede neural. As dimensões da camada de entrada, da camada oculta e da taxa de aprendizagem devem ser dadas ao executar a função. A inicialização dos pesos é realizada via ninicialização normal de Xavier sorteando valores na distribuição normal com média nula e desvio padrão igual a \(\sqrt{2/K+1}\) e para os pesos de entrada e da camada oculta respectivamente. No treinamento, o passo à frente simplesmente avalia a rede com os pesos atuais. O passo atrás calcula o erro ou resíduo na saída, calcula o gradiente e propaga o erro para a camada oculta. Em sequência os pesos são atualizados considerando a taxa de aprendizagem e calcula-se a função perda. O procedimento é repetido até alcançar o critério de parada, sendo este o número de iterações (epochs) definido.

# Classe para Rede Neural
NeuralNetwork <- function(input_size = 2, hidden_size = 8, learning_rate = 0.01) {
  
  # Inicialização dos pesos (normal Xavier initialization)
  w <- matrix(rnorm(hidden_size * (input_size + 1), 0, sqrt(2/(input_size + 1))), 
              nrow = hidden_size, ncol = input_size + 1)
  v <- matrix(rnorm(hidden_size + 1, 0, sqrt(2/(hidden_size + 1))), ncol = 1)
  
  # Forward pass
  forward <- function(X) {
    # Garantir que X seja matriz
    if (is.vector(X)) {
      X <- matrix(X, nrow = 1)
    }
    
    # X deve ser uma matriz n x 2 (x1, x2)
    n_samples <- nrow(X)
    
    # Adicionar bias (coluna de 1s) à entrada
    X_bias <- cbind(1, X)
    
    # Camada oculta: h_p = g(w_p0 + w_p1*x1 + w_p2*x2)
    z_hidden <- X_bias %*% t(w)  # n x hidden_size
    h_hidden <- relu(z_hidden)   # aplicar ReLU
    
    # Adicionar bias à camada oculta
    h_bias <- cbind(1, h_hidden)
    
    # Debug: verificar dimensões
    # cat(sprintf("Debug - h_bias: %d x %d, v: %d x %d\n", 
    #             nrow(h_bias), ncol(h_bias), nrow(v), ncol(v)))
    
    # Camada de saída: f(x) = v0 + sum(v_p * h_p)
    output <- h_bias %*% v
    
    return(list(output = output, h_hidden = h_hidden, z_hidden = z_hidden, X_bias = X_bias))
  }
  
  # Backward pass (backpropagation)
  backward <- function(X, y_true, forward_result) {
    n_samples <- nrow(X)
    
    # Extrair resultados do forward pass
    y_pred <- forward_result$output
    h_hidden <- forward_result$h_hidden
    z_hidden <- forward_result$z_hidden
    X_bias <- forward_result$X_bias
    
    # Erro na saída
    error_output <- y_pred - y_true
    
    # Gradientes para v (pesos da camada de saída)
    h_bias <- cbind(1, h_hidden)
    grad_v <- t(h_bias) %*% error_output / n_samples
    
    # Gradientes para w (pesos da camada oculta)
    # Propagação do erro para a camada oculta
    error_hidden <- (error_output %*% t(v[-1])) * relu_derivative(z_hidden)
    grad_w <- t(error_hidden) %*% X_bias / n_samples
    
    return(list(grad_v = grad_v, grad_w = grad_w))
  }
  
  # Função de perda (MSE)
  compute_loss <- function(X, y_true) {
    forward_result <- forward(X)
    y_pred <- forward_result$output
    mse <- mean((y_pred - y_true)^2)
    return(mse)
  }
  
  # Treinamento
  train <- function(X_train, y_train, X_val = NULL, y_val = NULL, epochs = 1000, verbose = F) {
    train_losses <- numeric(epochs)
    val_losses <- numeric(epochs)
    
    for (epoch in 1:epochs) {
      # Forward pass
      forward_result <- forward(X_train)
      
      # Backward pass
      gradients <- backward(X_train, y_train, forward_result)
      
      # Atualizar pesos
      v <<- v - learning_rate * gradients$grad_v
      w <<- w - learning_rate * gradients$grad_w
      
      # Calcular perdas
      train_loss <- compute_loss(X_train, y_train)
      train_losses[epoch] <- train_loss
      
      if (!is.null(X_val)) {
        val_loss <- compute_loss(X_val, y_val)
        val_losses[epoch] <- val_loss
      }
      
      # Imprimir progresso
      if (verbose && epoch %% 100 == 0) {
        cat(sprintf("Época %d: Perda treino = %.6f", epoch, train_loss))
        if (!is.null(X_val)) {
          cat(sprintf(", Perda validação = %.6f", val_loss))
        }
        cat("\n")
      }
    }
    
    return(list(train_losses = train_losses, val_losses = val_losses))
  }
  
  # Predição
  predict <- function(X) {
    forward_result <- forward(X)
    return(forward_result$output)
  }
  
  # Retornar lista de funções
  list(
    forward = forward,
    backward = backward,
    compute_loss = compute_loss,
    train = train,
    predict = predict,
    get_weights = function() list(w = w, v = v)
  )
}

A seguir é realizado o treinamento considerando s dados separados para treino. Sugere-se testar outros valores de número de neurônios na camada oculta (hidden_size), taxa de aprendizagem e epochs.

# Criar e treinar a rede neural
cat("Criando rede neural com 1 camada oculta e 8 neurônios...\n")

Criando rede neural com 1 camada oculta e 8 neurônios...

nn <- NeuralNetwork(input_size = 2, hidden_size = 8, learning_rate = 0.01)

# Preparar dados de treino
X_train <- cbind(x1_train, x2_train)
X_test <- cbind(x1_test, x2_test)

# Debug: verificar dimensões
cat("Dimensões dos dados:\n")

Dimensões dos dados:

cat(sprintf("X_train: %d x %d\n", nrow(X_train), ncol(X_train)))

X_train: 800 x 2

cat(sprintf("y_train: %d\n", length(y_train)))

y_train: 800

cat(sprintf("X_test: %d x %d\n", nrow(X_test), ncol(X_test)))

X_test: 200 x 2

cat(sprintf("y_test: %d\n", length(y_test)))

y_test: 200

# Treinar o modelo
cat("Iniciando treinamento...\n")

Iniciando treinamento...

history <- nn$train(X_train, y_train, X_test, y_test, epochs = 2000, verbose = F)

Em seguida avalia-se o desempenho do modelo obtido.

# Fazer predições
y_pred_train <- nn$predict(X_train)
y_pred_test <- nn$predict(X_test)

# Calcular métricas
rmse_train <- sqrt(mean((y_pred_train - y_train)^2))
rmse_test <- sqrt(mean((y_pred_test - y_test)^2))
r2_train <- 1 - sum((y_train - y_pred_train)^2)/sum((y_train - mean(y_train))^2)
r2_test <- 1 - sum((y_test - y_pred_test)^2)/sum((y_test - mean(y_test))^2)

cat("\n=== RESULTADOS ===\n")


=== RESULTADOS ===

cat(sprintf("RMSE Treino: %.4f\n", rmse_train))

RMSE Treino: 0.2013

cat(sprintf("RMSE Teste: %.4f\n", rmse_test))

RMSE Teste: 0.2036

cat(sprintf("R² Treino: %.4f\n", r2_train))

R² Treino: 0.9588

cat(sprintf("R² Teste: %.4f\n", r2_test))

R² Teste: 0.9606

Alguns gráficos são implementados conforme segue.

# Gráfico 1: Curva de aprendizado
epochs <- 1:length(history$train_losses)
loss_data <- data.frame(
  Epoch = rep(epochs, 2),
  Loss = c(history$train_losses, history$val_losses),
  Type = rep(c("Treino", "Validação"), each = length(epochs))
)

p1 <- ggplot(loss_data, aes(x = Epoch, y = Loss, color = Type)) +
  geom_line(size = 1) +
  labs(y = "Perda (MSE)", color ="") +
  scale_color_manual(values = c("Treino" = "blue", "Validação" = "red")) +
scale_linetype_manual(values = c("Treino" = 1, "Validação" = 3)) + 
  ylim(0,0.2)

Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

# Gráfico 2: Predições vs Valores Reais (Treino)
pred_data_train <- data.frame(
  Real = y_train,
  Predito = as.vector(y_pred_train)
)

p2 <- ggplot(pred_data_train, aes(x = Real, y = Predito)) +
  geom_point(alpha = 0.2, color = "blue") +
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
  labs(subtitle = paste("Treino (R² =", round(r2_train, 3), ")"),
       x = "Observado")

# Gráfico 3: Predições vs Valores Reais (Teste)
pred_data_test <- data.frame(
  Real = y_test,
  Predito = as.vector(y_pred_test)
)

p3 <- ggplot(pred_data_test, aes(x = Real, y = Predito)) +
  geom_point(alpha = 0.2, color = "darkgreen") +
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
  labs(subtitle = paste("Teste (R² =", round(r2_test, 3), ")"),
       x = "Observado")

# Gráfico 4: Superfície de predição (para visualizar a função aprendida)
# Criar grade de pontos
x1_grid <- seq(min(x1_scaled), max(x1_scaled), length.out = 50)
x2_grid <- seq(min(x2_scaled), max(x2_scaled), length.out = 50)
grid <- expand.grid(x1 = x1_grid, x2 = x2_grid)
X_grid <- as.matrix(grid)
y_grid <- nn$predict(X_grid)

grid$y_pred <- as.vector(y_grid)

p4 <- ggplot(grid, aes(x = x1, y = x2, fill = y_pred)) +
  geom_tile() +
  scale_fill_gradient2(low = "blue", mid = "white", high = "red", midpoint = 0)

A Figura 11.2 plota a evolução da função perda para os dados de treino e de teste.

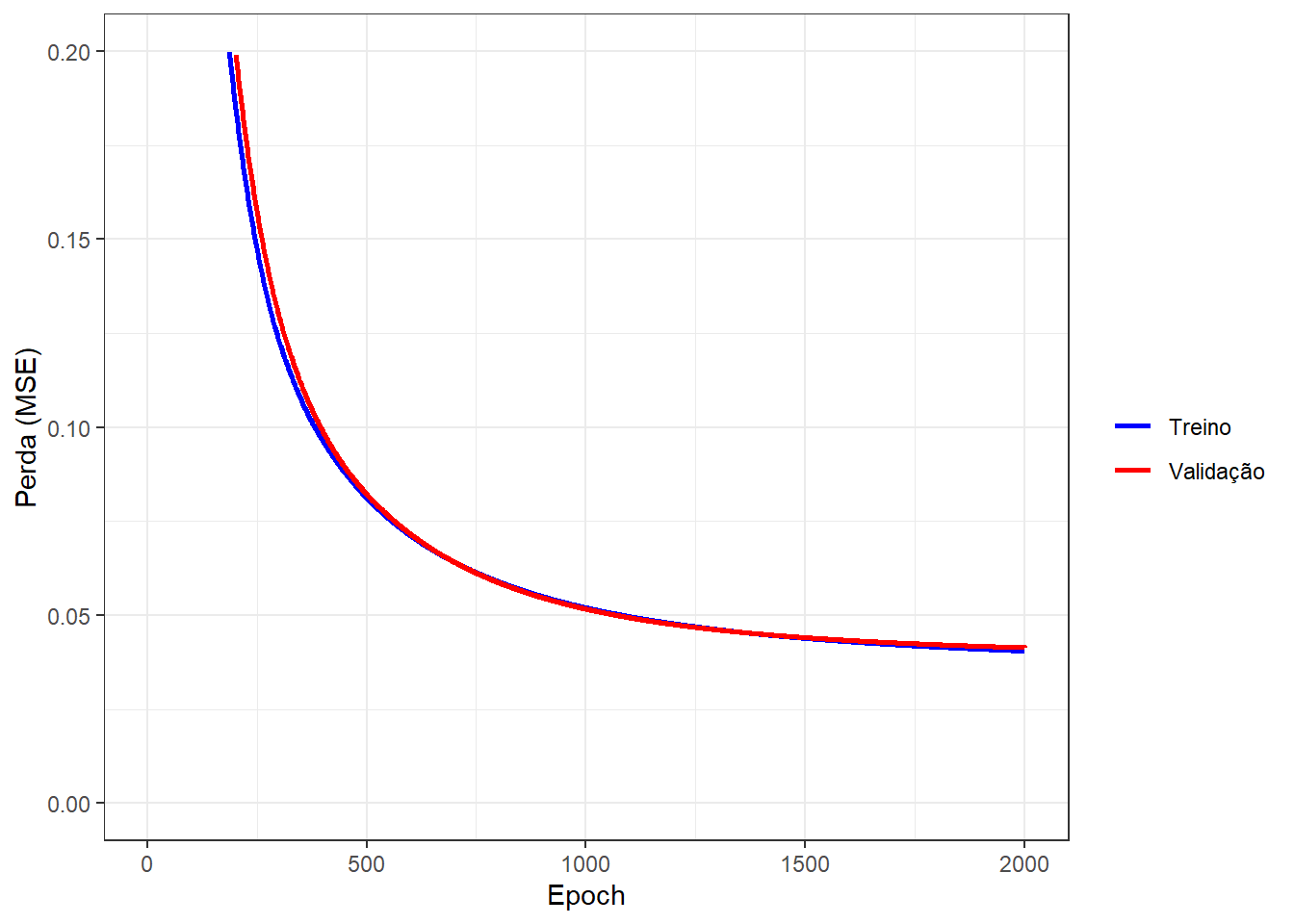
Figura 11.2: Função perda para treino e teste versus epochs

A Figura 11.3 plota as previsões versus as observações para os dados de treino e de teste.

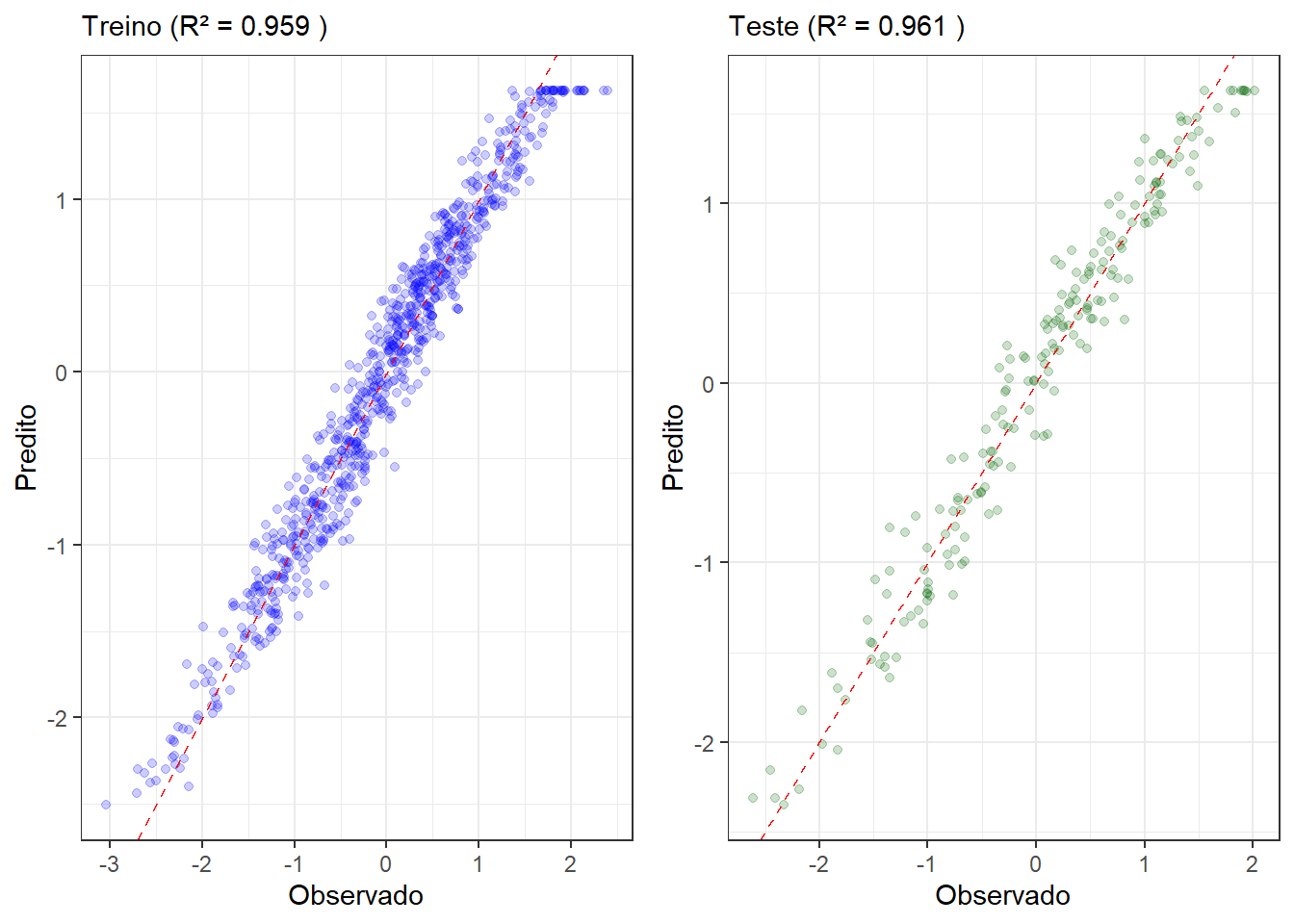
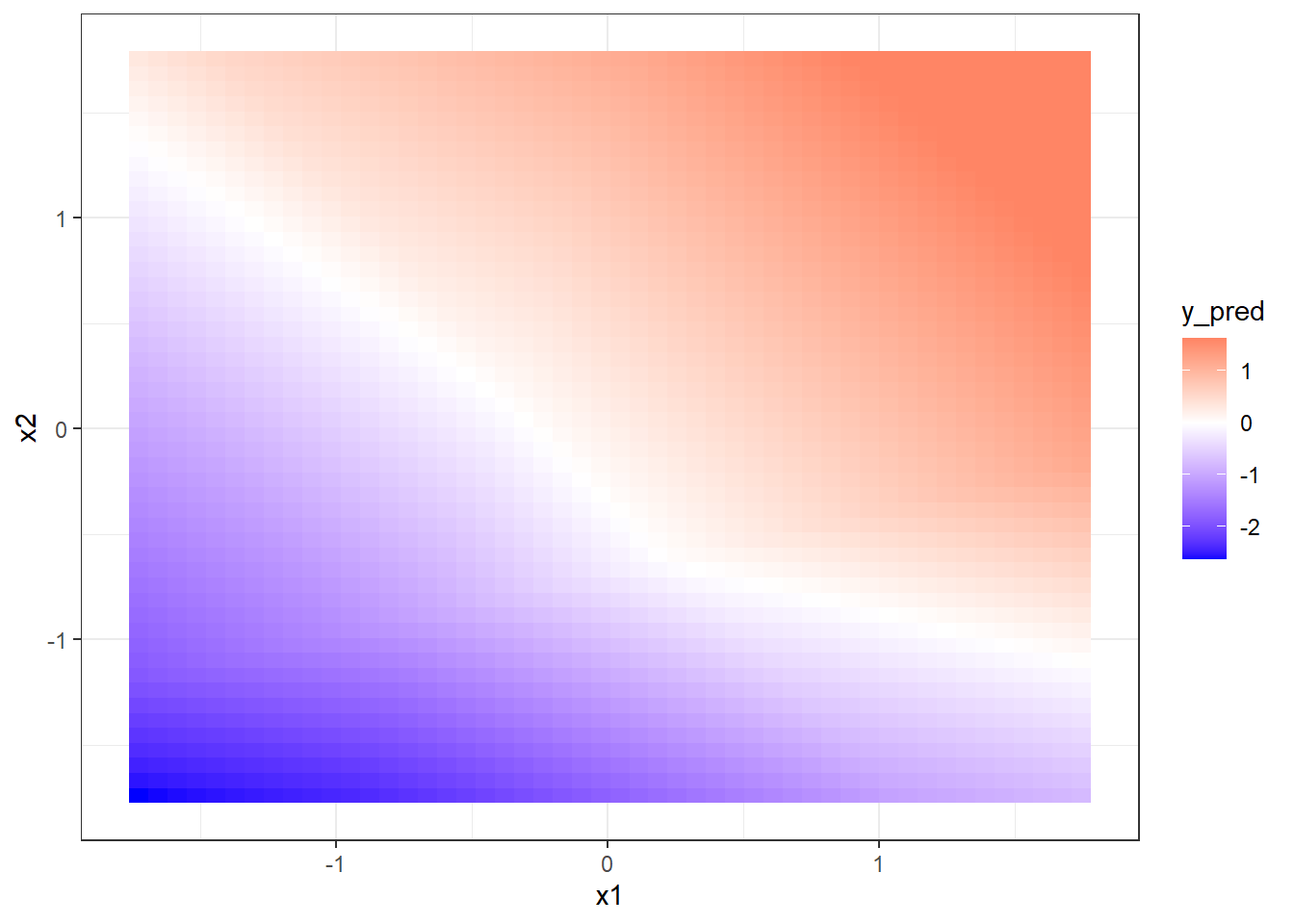
A Figura 11.4 plota o gráfico de contorno para a rede neural obtida.

Figura 11.4: Gráfico de contorno do modelo obtido

Aqui é realizada uma comparação com um modelo de regressão linear múltipla.

# Ajustar modelo linear para comparação
lm_model <- lm(y_train ~ x1_train + x2_train)
y_pred_lm_train <- predict(lm_model)
y_pred_lm_test <- predict(lm_model, newdata = data.frame(x1_train = x1_test, x2_train = x2_test))

rmse_lm_train <- sqrt(mean((y_pred_lm_train - y_train)^2))
rmse_lm_test <- sqrt(mean((y_pred_lm_test - y_test)^2))
r2_lm_train <- summary(lm_model)$r.squared
r2_lm_test <- 1 - sum((y_test - y_pred_lm_test)^2)/sum((y_test - mean(y_test))^2)

cat("\n=== COMPARAÇÃO COM REGRESSÃO LINEAR ===\n")


=== COMPARAÇÃO COM REGRESSÃO LINEAR ===

cat("Rede Neural:\n")

Rede Neural:

cat(sprintf("  RMSE Teste: %.4f, R² Teste: %.4f\n", rmse_test, r2_test))

  RMSE Teste: 0.2036, R² Teste: 0.9606

cat("Regressão Linear:\n")

Regressão Linear:

cat(sprintf("  RMSE Teste: %.4f, R² Teste: %.4f\n", rmse_lm_test, r2_lm_test))

  RMSE Teste: 0.2487, R² Teste: 0.9412

Por fim, são apresentados os pesos ótimos obtidos para a rede.

weights <- nn$get_weights()
cat("\n=== PESOS DA REDE NEURAL ===\n")


=== PESOS DA REDE NEURAL ===

cat("Pesos da camada oculta (w):\n")

Pesos da camada oculta (w):

print(round(weights$w, 4))

             x1_train x2_train
[1,]  1.9242  -0.8116  -0.6826
[2,] -0.5910  -0.3866  -0.2250
[3,] -0.1675  -0.8945  -0.6355
[4,] -0.3704   0.0516  -0.0623
[5,] -1.2383  -0.2510  -0.6065
[6,] -2.1539  -0.1231  -0.5666
[7,] -0.5086  -1.2340   0.3557
[8,] -0.8132   0.3516  -1.1909

cat("\nPesos da camada de saída (v):\n")


Pesos da camada de saída (v):

print(round(weights$v, 4))

         [,1]
 [1,]  1.6279
 [2,] -0.7421
 [3,]  0.3169
 [4,] -0.3611
 [5,]  0.1283
 [6,]  0.3160
 [7,]  0.5798
 [8,]  0.1635
 [9,] -0.6135

11.4 Validação cruzada e grid search para treinar múltiplos modelos de regressão passo a passo via `tidymodels`

Previsão do preço de computadores.

library(Ecdat) # para dados
library(tidymodels) 
library(modelsummary)
library(finetune) # para grid search
library(dplyr)
library(baguette) # bag_tree

Leitura de dados.

data(Computers)
dados2 <- na.omit(Computers)

Entendendo os dados.

dados2 |> glimpse()

Rows: 6,259
Columns: 10
$ price   <dbl> 1499, 1795, 1595, 1849, 3295, 3695, 1720, 1995, 2225, 2575, 21…
$ speed   <dbl> 25, 33, 25, 25, 33, 66, 25, 50, 50, 50, 33, 66, 50, 25, 50, 50…
$ hd      <dbl> 80, 85, 170, 170, 340, 340, 170, 85, 210, 210, 170, 210, 130, …
$ ram     <dbl> 4, 2, 4, 8, 16, 16, 4, 2, 8, 4, 8, 8, 4, 8, 8, 4, 2, 4, 4, 8, …
$ screen  <dbl> 14, 14, 15, 14, 14, 14, 14, 14, 14, 15, 15, 14, 14, 14, 14, 14…
$ cd      <fct> no, no, no, no, no, no, yes, no, no, no, no, no, no, no, no, n…
$ multi   <fct> no, no, no, no, no, no, no, no, no, no, no, no, no, no, no, no…
$ premium <fct> yes, yes, yes, no, yes, yes, yes, yes, yes, yes, yes, yes, yes…
$ ads     <dbl> 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94, 94…
$ trend   <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…

Estatísticas descritivas.

datasummary_skim(dados2)

	Unique	Missing Pct.	Mean	SD	Min	Median	Max
price	808	0	2219.6	580.8	949.0	2144.0	5399.0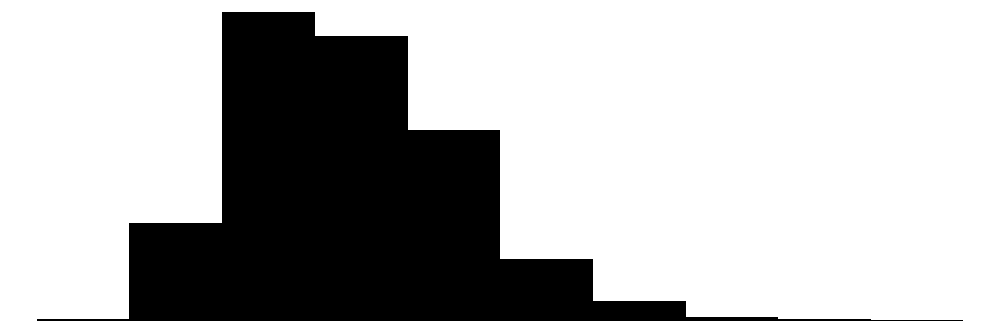
speed	6	0	52.0	21.2	25.0	50.0	100.0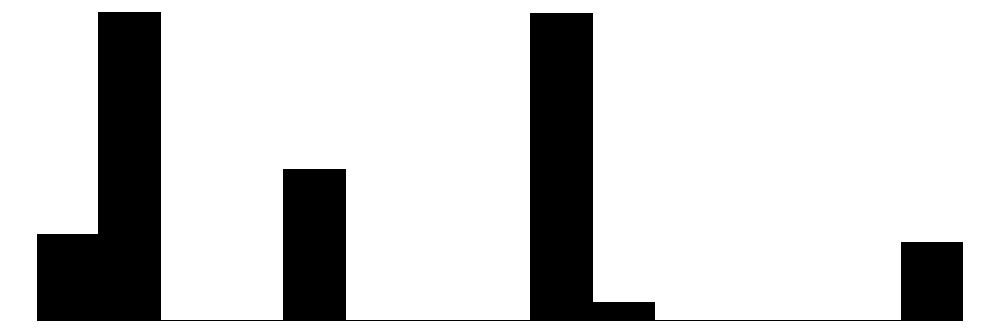
hd	59	0	416.6	258.5	80.0	340.0	2100.0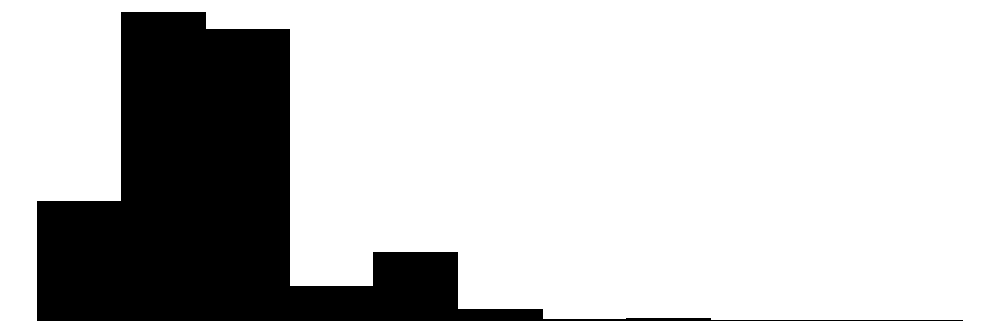
ram	6	0	8.3	5.6	2.0	8.0	32.0
screen	3	0	14.6	0.9	14.0	14.0	17.0
ads	34	0	221.3	74.8	39.0	246.0	339.0
trend	35	0	15.9	7.9	1.0	16.0	35.0
		N	%
cd	no	3351	53.5
	yes	2908	46.5
multi	no	5386	86.1
	yes	873	13.9
premium	no	612	9.8
	yes	5647	90.2

Criando coluna com combinações das variáveis categóricas que tem níveis desbalanceados.

dados2 <- dados2 |>
  mutate(multi_premium = paste(multi, premium,  
                               sep = '_'))

Separando dados de treino e teste.

set.seed(16)
dados_split2 <- initial_split(dados2, 
                              prop = 0.25,
                              strata = multi_premium)
  
dados_train2 <- training(dados_split2)
dados_test2  <- testing(dados_split2)

set.seed(17)
dados_folds2 <- 
  vfold_cv(v = 10, dados_train2, repeats = 2)

Definindo a receita. A receita cntém o modelo, além dos preprocessamentos realizados nas variáveis preditoras.

normalized_rec2 <- 
  recipe(price ~ speed + hd + ram + screen + cd + multi + premium + ads + trend, 
         data = dados_train2) |> 
  step_normalize(all_numeric_predictors()) |>
  step_dummy(all_nominal_predictors())

Definindo os métodos de regressão a serem testados. Deve-se definir os hiperparâmetros a serem testados e o pacote (engine), uma vez que geralmente há várias opções de pacotes em R para um mesmo método.

linear_reg_spec <- 
  linear_reg(penalty = tune(), mixture = tune()) |> 
  set_engine("glmnet")

tree_spec <- decision_tree(tree_depth = tune(), min_n = tune(), cost_complexity = tune()) |> 
  set_engine("rpart") |> 
  set_mode("regression")

bag_cart_spec <- 
   bag_tree(tree_depth = tune(), min_n = tune(), cost_complexity = tune()) |> 
   set_engine("rpart") |> 
   set_mode("regression")

rforest_spec <- rand_forest(mtry = tune(), min_n = tune(), trees = tune()) |> 
  set_engine("ranger") |> 
  set_mode("regression")

xgb_spec <- # evolution of GBM
  boost_tree(tree_depth = tune(), learn_rate = tune(), loss_reduction = tune(), 
             min_n = tune(), sample_size = tune(), trees = tune()) |> 
  set_engine("xgboost") |> 
  set_mode("regression")

svm_r_spec <- 
  svm_rbf(cost = tune(), rbf_sigma = tune()) |> 
  set_engine("kernlab") |> 
  set_mode("regression")

svm_p_spec <- 
  svm_poly(cost = tune(), degree = tune()) |> 
  set_engine("kernlab") |> 
  set_mode("regression")

mars_spec <- # method similar to GAM
   mars(prod_degree = tune()) %>%  
   set_engine("earth") %>% 
   set_mode("regression")

nnet_spec <- 
  mlp(hidden_units = tune(), penalty = tune(), epochs = tune()) |> 
  set_engine("nnet", MaxNWts = 2600) |> 
  set_mode("regression")

nnet_param <- 
  nnet_spec |> 
  extract_parameter_set_dials() |> 
  update(hidden_units = hidden_units(c(1, 27)))

Definindo o workflow. O workflow contém a receita e os modelos.

normalized2 <- 
  workflow_set(
    preproc = list(normalized = normalized_rec2), 
    models = list(linear_reg = linear_reg_spec,
                  tree = tree_spec,
                  bagging = bag_cart_spec,
                  rforest = rforest_spec,
                  XGB = xgb_spec,
                  SVM_radial = svm_r_spec, 
                  SVM_poly = svm_p_spec,
                  MARS = mars_spec,
                  neural_network = nnet_spec)
  )
normalized2

# A workflow set/tibble: 9 × 4
  wflow_id                  info             option    result    
  <chr>                     <list>           <list>    <list>    
1 normalized_linear_reg     <tibble [1 × 4]> <opts[0]> <list [0]>
2 normalized_tree           <tibble [1 × 4]> <opts[0]> <list [0]>
3 normalized_bagging        <tibble [1 × 4]> <opts[0]> <list [0]>
4 normalized_rforest        <tibble [1 × 4]> <opts[0]> <list [0]>
5 normalized_XGB            <tibble [1 × 4]> <opts[0]> <list [0]>
6 normalized_SVM_radial     <tibble [1 × 4]> <opts[0]> <list [0]>
7 normalized_SVM_poly       <tibble [1 × 4]> <opts[0]> <list [0]>
8 normalized_MARS           <tibble [1 × 4]> <opts[0]> <list [0]>
9 normalized_neural_network <tibble [1 × 4]> <opts[0]> <list [0]>

all_workflows2 <- 
  bind_rows(normalized2) |> 
  # Make the workflow ID's a little more simple: 
  mutate(wflow_id = gsub("(simple_)|(normalized_)", "", wflow_id))
all_workflows2

# A workflow set/tibble: 9 × 4
  wflow_id       info             option    result    
  <chr>          <list>           <list>    <list>    
1 linear_reg     <tibble [1 × 4]> <opts[0]> <list [0]>
2 tree           <tibble [1 × 4]> <opts[0]> <list [0]>
3 bagging        <tibble [1 × 4]> <opts[0]> <list [0]>
4 rforest        <tibble [1 × 4]> <opts[0]> <list [0]>
5 XGB            <tibble [1 × 4]> <opts[0]> <list [0]>
6 SVM_radial     <tibble [1 × 4]> <opts[0]> <list [0]>
7 SVM_poly       <tibble [1 × 4]> <opts[0]> <list [0]>
8 MARS           <tibble [1 × 4]> <opts[0]> <list [0]>
9 neural_network <tibble [1 × 4]> <opts[0]> <list [0]>

Realizando grid search e validação cruzada.

race_ctrl <-
  control_race(
    save_pred = TRUE,
    parallel_over = "everything",
    save_workflow = TRUE
  )

race_results2 <-
  all_workflows2 |>
  workflow_map(
    "tune_race_anova",
    seed = 1503,
    resamples = dados_folds2,
    grid = 25,
    control = race_ctrl
  )

→ A | warning: A correlation computation is required, but `estimate` is constant and has 0
               standard deviation, resulting in a divide by 0 error. `NA` will be returned.

There were issues with some computations   A: x1

There were issues with some computations   A: x9

There were issues with some computations   A: x16

There were issues with some computations   A: x26

There were issues with some computations   A: x27
There were issues with some computations   A: x27

Extraindo métricas para avaliar os resultados da validação cruzada.

collect_metrics(race_results2) |> 
  filter(.metric == "rmse") |>
  arrange(mean)

# A tibble: 37 × 9
   wflow_id       .config   preproc model .metric .estimator  mean     n std_err
   <chr>          <chr>     <chr>   <chr> <chr>   <chr>      <dbl> <int>   <dbl>
 1 XGB            Preproce… recipe  boos… rmse    standard    173.    20    3.20
 2 rforest        Preproce… recipe  rand… rmse    standard    197.    20    3.80
 3 SVM_poly       Preproce… recipe  svm_… rmse    standard    213.    20    3.60
 4 bagging        Preproce… recipe  bag_… rmse    standard    214.    20    4.10
 5 bagging        Preproce… recipe  bag_… rmse    standard    216.    20    4.63
 6 SVM_radial     Preproce… recipe  svm_… rmse    standard    219.    20    4.58
 7 MARS           Preproce… recipe  mars  rmse    standard    230.    20    3.47
 8 tree           Preproce… recipe  deci… rmse    standard    247.    20    5.51
 9 neural_network Preproce… recipe  mlp   rmse    standard    259.    20   11.6 
10 neural_network Preproce… recipe  mlp   rmse    standard    261.    20    7.00
# ℹ 27 more rows

collect_metrics(race_results2) |> 
  filter(.metric == "rsq") |>
  arrange(desc(mean))

# A tibble: 37 × 9
   wflow_id       .config   preproc model .metric .estimator  mean     n std_err
   <chr>          <chr>     <chr>   <chr> <chr>   <chr>      <dbl> <int>   <dbl>
 1 XGB            Preproce… recipe  boos… rsq     standard   0.912    20 0.00315
 2 rforest        Preproce… recipe  rand… rsq     standard   0.887    20 0.00331
 3 SVM_poly       Preproce… recipe  svm_… rsq     standard   0.866    20 0.00511
 4 bagging        Preproce… recipe  bag_… rsq     standard   0.865    20 0.00420
 5 bagging        Preproce… recipe  bag_… rsq     standard   0.862    20 0.00444
 6 SVM_radial     Preproce… recipe  svm_… rsq     standard   0.859    20 0.00515
 7 MARS           Preproce… recipe  mars  rsq     standard   0.844    20 0.00454
 8 tree           Preproce… recipe  deci… rsq     standard   0.819    20 0.00802
 9 neural_network Preproce… recipe  mlp   rsq     standard   0.798    20 0.0108 
10 neural_network Preproce… recipe  mlp   rsq     standard   0.795    20 0.0206 
# ℹ 27 more rows

Visualizando desempenho dos métodos.

IC_rmse2 <- collect_metrics(race_results2) |> 
  filter(.metric == "rmse") |> 
  group_by(wflow_id) |>
  filter(mean == min(mean)) |>
  group_by(wflow_id) |> 
  arrange(mean) |> 
  ungroup()

IC_r22 <- collect_metrics(race_results2) |> 
  filter(.metric == "rsq") |> 
  group_by(wflow_id) |>
  filter(mean == max(mean)) |>
  group_by(wflow_id) |> 
  arrange(desc(mean)) |> 
  ungroup() 

IC2 <- bind_rows(IC_rmse2, IC_r22)

ggplot(IC2, aes(x = factor(wflow_id, levels = unique(wflow_id)), y = mean)) +
  facet_wrap(~.metric, scales = "free") +
  geom_point(stat="identity", aes(color = wflow_id), pch = 1) +
  geom_errorbar(stat="identity", aes(color = wflow_id, 
                                     ymin=mean-1.96*std_err,
                                     ymax=mean+1.96*std_err), width=.2) + 
  labs(y = "", x = "method") + theme_bw() +
  theme(legend.position = "none",
        axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))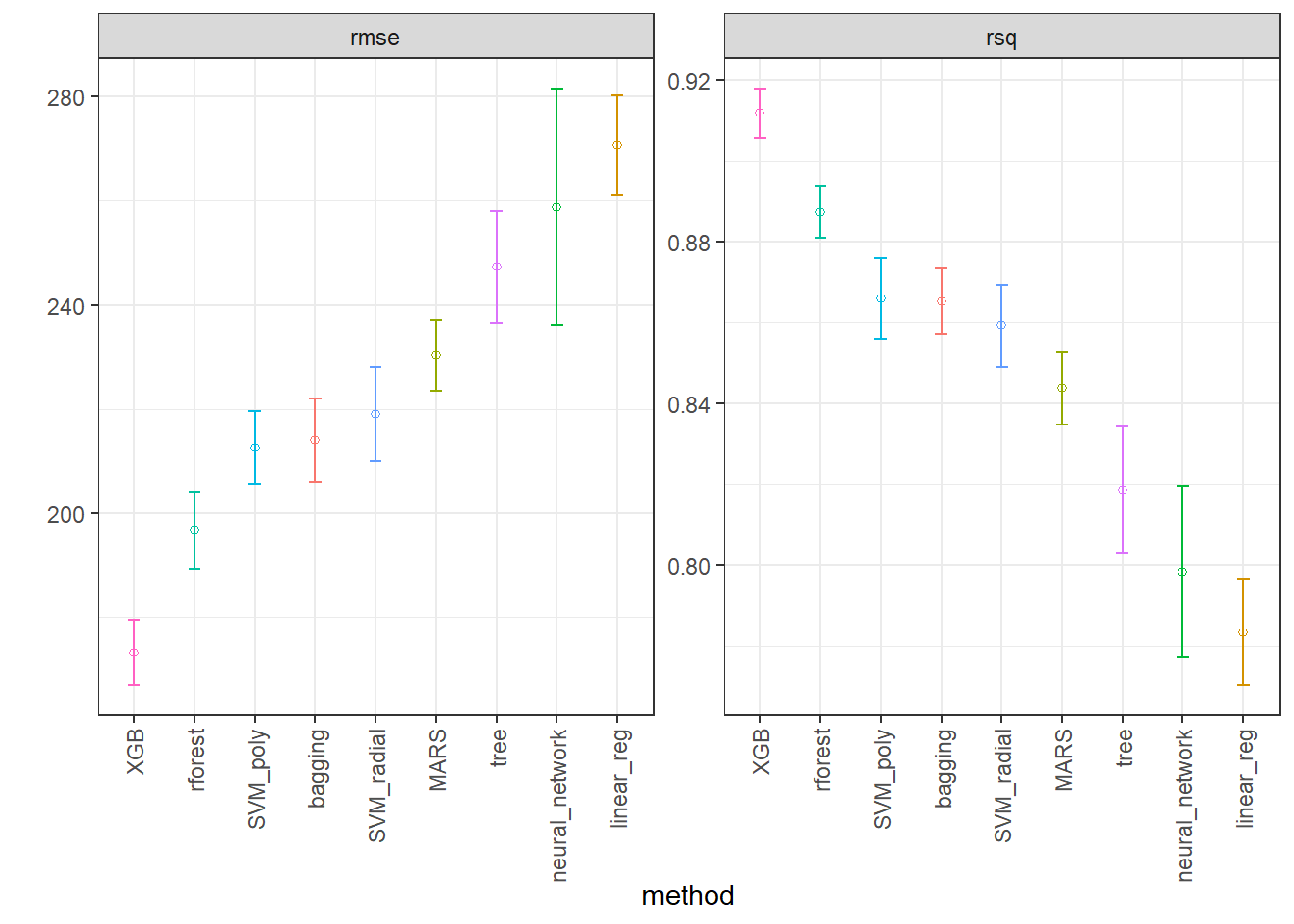

Obtendo níveis ótimos dos hiperparâmetros do melhor modelo.

best_rmse2 <- 
  race_results2 |> 
  extract_workflow_set_result("XGB") |> 
  select_best(metric = "rmse")
best_rmse2

# A tibble: 1 × 7
  trees min_n tree_depth learn_rate loss_reduction sample_size .config          
  <int> <int>      <int>      <dbl>          <dbl>       <dbl> <chr>            
1  1416     9          5     0.0226           3.48       0.962 Preprocessor1_Mo…

XGB_test_results <- 
  race_results2 |> 
  extract_workflow("XGB") |> 
  finalize_workflow(best_rmse2) |> 
  last_fit(split = dados_split2)

collect_metrics(XGB_test_results)

# A tibble: 2 × 4
  .metric .estimator .estimate .config             
  <chr>   <chr>          <dbl> <chr>               
1 rmse    standard     170.    Preprocessor1_Model1
2 rsq     standard       0.915 Preprocessor1_Model1

Plotando previstos versus observados para os dados de teste dos dois melhores métodos.

best_rmse2_2 <- 
  race_results2 |> 
  extract_workflow_set_result("rforest") |> 
  select_best(metric = "rmse")
best_rmse2_2

# A tibble: 1 × 4
   mtry trees min_n .config              
  <int> <int> <int> <chr>                
1     6  1167     2 Preprocessor1_Model17

rf_test_results <- 
  race_results2 |> 
  extract_workflow("rforest") |> 
  finalize_workflow(best_rmse2_2) |> 
  last_fit(split = dados_split2)

collect_metrics(rf_test_results)

# A tibble: 2 × 4
  .metric .estimator .estimate .config             
  <chr>   <chr>          <dbl> <chr>               
1 rmse    standard     196.    Preprocessor1_Model1
2 rsq     standard       0.888 Preprocessor1_Model1

test_results2 <- rbind(XGB_test_results |>
                        collect_predictions(),
                       rf_test_results |>
                        collect_predictions())

test_results2$method <- c(rep("XGB", nrow(XGB_test_results |>
                        collect_predictions())),
                         rep("rforest", nrow(rf_test_results |>
                        collect_predictions())))

test_results2 |>
  ggplot(aes(x = price, y = .pred)) + 
  geom_abline(color = "gray50", lty = 2) + 
  geom_point(alpha = 0.2) + 
  facet_grid(col = vars(method)) +
  coord_obs_pred() + 
  labs(x = "observed", y = "predicted") + 
  theme_bw()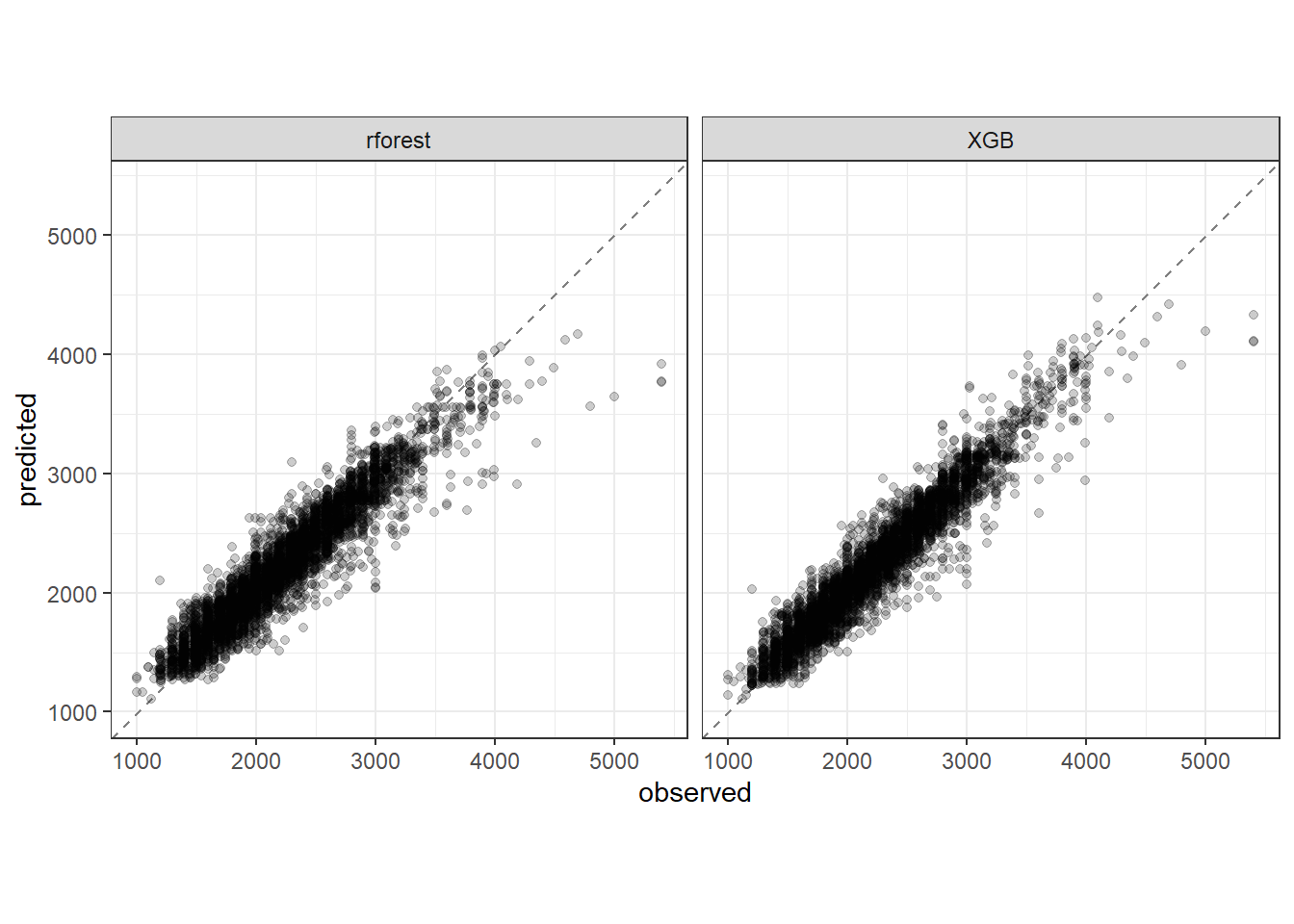

Modelo final.

XGB_final <- race_results2 |> 
  extract_workflow("XGB") |> 
  finalize_workflow(best_rmse2)
XGB_final

══ Workflow ════════════════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: boost_tree()

── Preprocessor ────────────────────────────────────────────────────────────────
2 Recipe Steps

• step_normalize()
• step_dummy()

── Model ───────────────────────────────────────────────────────────────────────
Boosted Tree Model Specification (regression)

Main Arguments:
  trees = 1416
  min_n = 9
  tree_depth = 5
  learn_rate = 0.0226030302714192
  loss_reduction = 3.48070058842842
  sample_size = 0.9625

Computational engine: xgboost

Referências

Bishop, Christopher M., and Hugh Bishop. “Deep learning: foundations and concepts.” (2024).

Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An introduction to statistical learning: with applications in R. Spinger.

11.1 Definições iniciais

11.2 Descida do gradiente e propagação para trás

11.3 Implementação de uma rede neural para regressão passo a passo na linguagem R

11.4 Validação cruzada e grid search para treinar múltiplos modelos de regressão passo a passo via tidymodels

Referências

11.4 Validação cruzada e grid search para treinar múltiplos modelos de regressão passo a passo via `tidymodels`