7 Regressão dinâmica
7.1 Modelos com erro aproximado por ARIMA
Os modelos de regressão dinâmica possibilitam a inclusão de variáveis ou séries temporais regressoras ou independentes, além de modelar o resíduo da regressão via ARIMA, unindo as capacidades dos métodos expostos nos capítulos 4 e 6. Um modelo de regressão dinâmica pode ser expresso conforme Equação 7.1, onde \(\varepsilon_t\) é ruído branco. Ou seja, o modelo permite que os resíduos do modelo de regressão, agora denominados \(\eta_t\), sejam autocorrelacionados, sendo esta autocorrelação seja tratada por um modelo ARIMA. Pode-se observar que o modelo de regressão contempla de uma até \(k\) séries temporais regressoras, \(x_{t1}, \ldots, x_{tk}\).
\[ \begin{matrix} y_t = \beta_0 + \beta_1x_{t1} + \cdots + \beta_kx_{tk} + \eta_t, \\ (1-\phi_1B- \ldots - \phi_pB^p)(1-B)^d\eta_t = c+( 1+\theta_1B+\ldots+\theta_qB^q)\varepsilon_t \end{matrix} \tag{7.1}\]
Os coeficientes de regressão, \(\beta_0, \ldots, \beta_k\), e do modelo ARIMA, \(\phi_1B, \ldots, \phi_p, \theta_1, \ldots, \theta_q\) são estimados em conjunto minimizando \(\varepsilon_t\) . A estimativa isolada dos coeficientes de regressão minimizando \(\eta_t\) acarretaria diversos problemas no modelo. É importante também que a série a ser predita e as regressoras sejam estacionárias, de forma que o grau de diferenciação \(d\) necessário para se obter a estacionariedade seja aplicado.
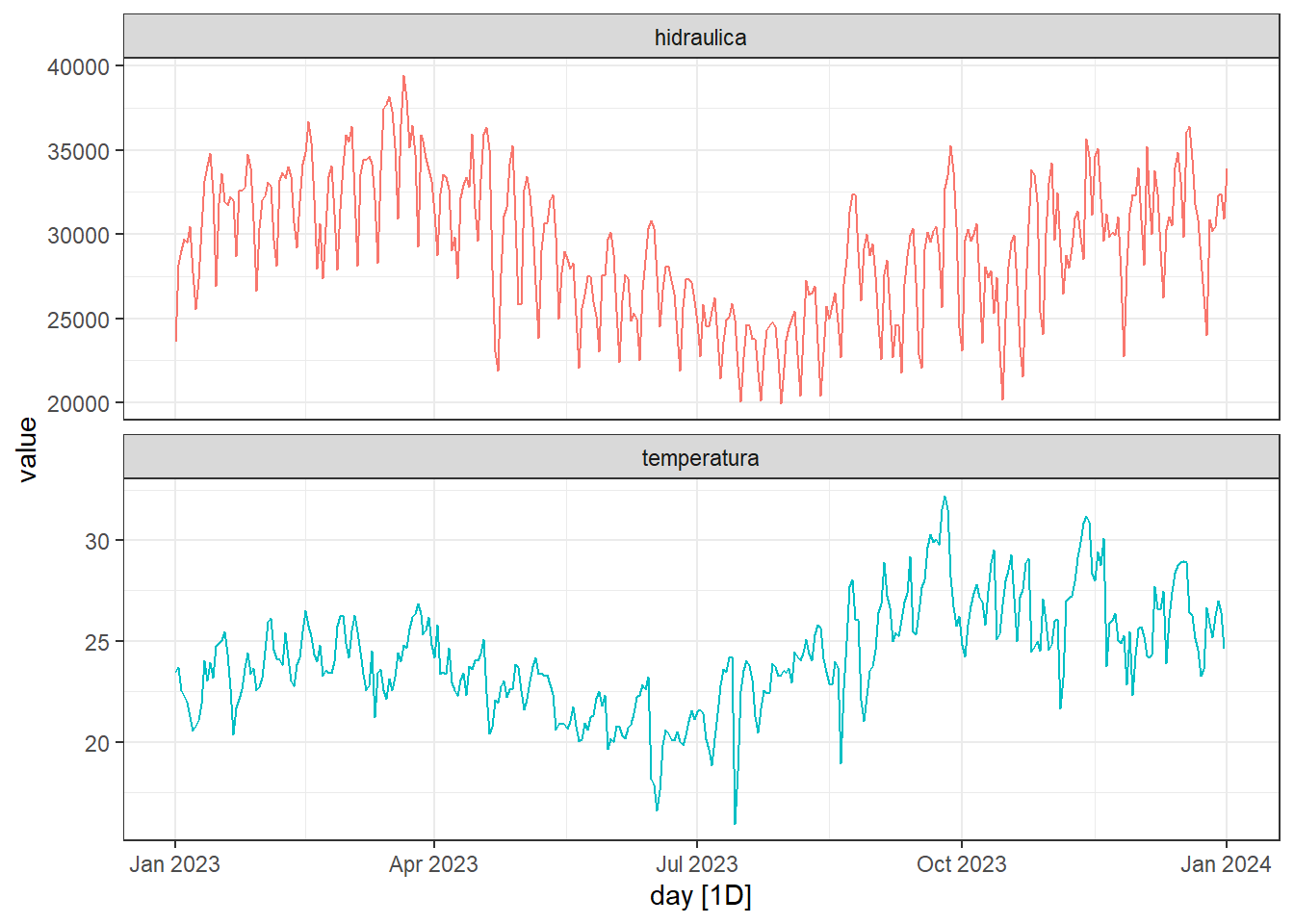
A Figura 7.1 plota séries temporais com frequência diária para o ano de 2023 do consumo médio de eletricidade advinda de geração hidráulica no subsistema do sudeste e centro oeste do Brasil e de temperatura média diária da cidade de Uberlândia em Minas Gerais. Tal cidade foi considerada por ser uma que representa bem a temperatura média de ambas as regiões dentre as monitoras pelo INMET. Pode-se sugerir um modelo de regressão dinâmica para o consumo diário de energia em função da temperatura média diária, descrevendo os erros com um modelo ARIMA.
A seguir expõe-se o resultado obtido.
Series: hidraulica
Model: LM w/ ARIMA(3,0,2)(0,1,1)[7] errors
Coefficients:
ar1 ar2 ar3 ma1 ma2 sma1 temperatura
1,1881 -0,9818 0,5842 -0,2459 0,542 -0,8142 201,8885
s.e. 0,1905 0,2335 0,1772 0,1885 0,285 0,0695 106,5817
sigma^2 estimated as 7374424: log likelihood=-3208,93
AIC=6433,85 AICc=6434,28 BIC=6464,58O modelo obtido pode ser expresso conforme segue.
\[ \begin{align} y_t &= 62.7853x_t + \eta_t\\ (1-1,76B+0.96B^2-0.19B^3)(1+0.0487B^{7})\eta_t &= (1+0.8358B)( 1+0.9290B^{7})\varepsilon_t \end{align} \]
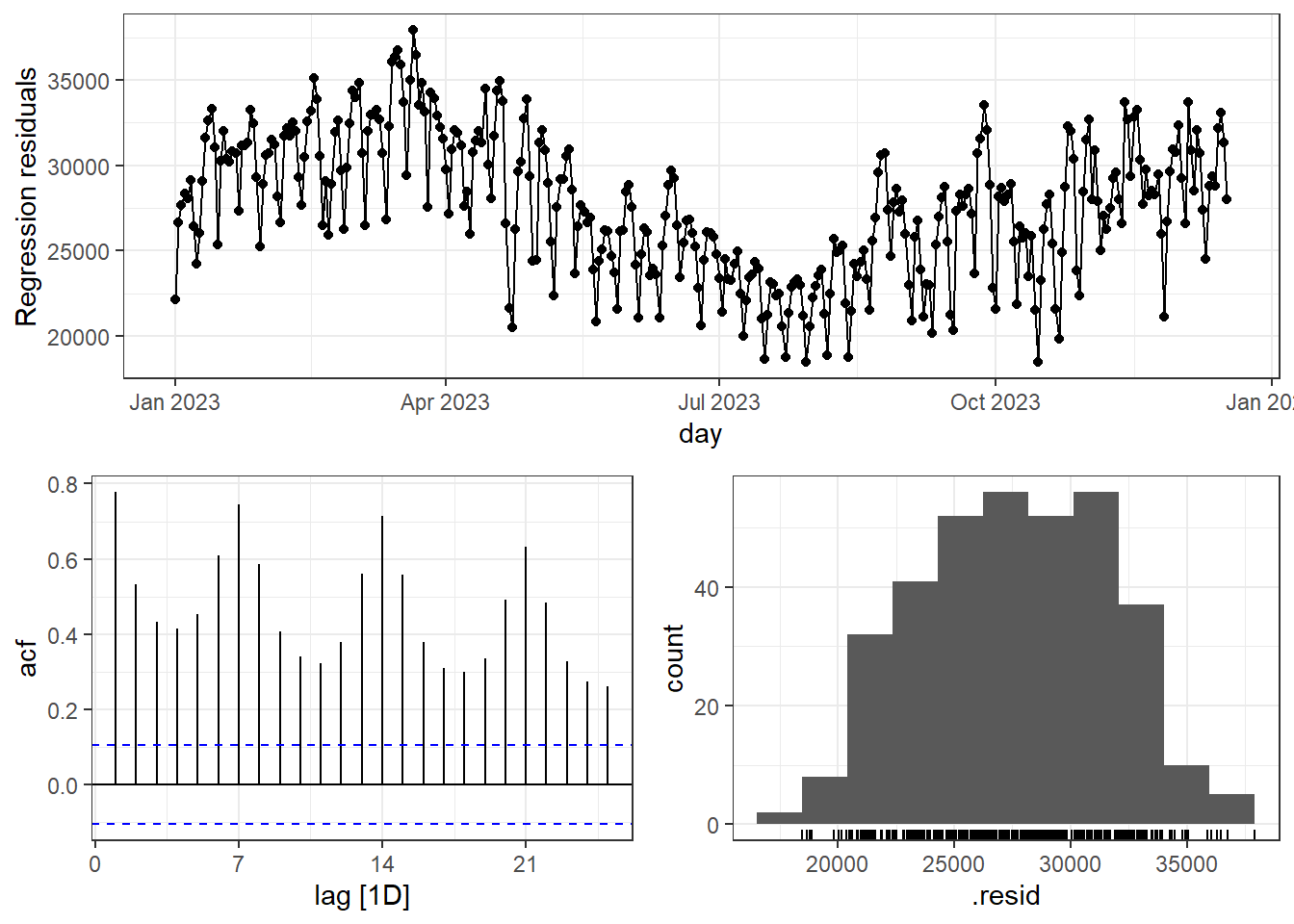
Os resíduos do modelo ARIMA, \(\varepsilon_t\) devem apresentar padrão de ruído branco. Já os de regressão, \(\eta_t\), não apresentam pressuposição. A Figura 7.2 apresenta os gráficos de resíduos para \(\eta_t\). Observa-se autocorrelação e padrão de sazonalidade semanal.
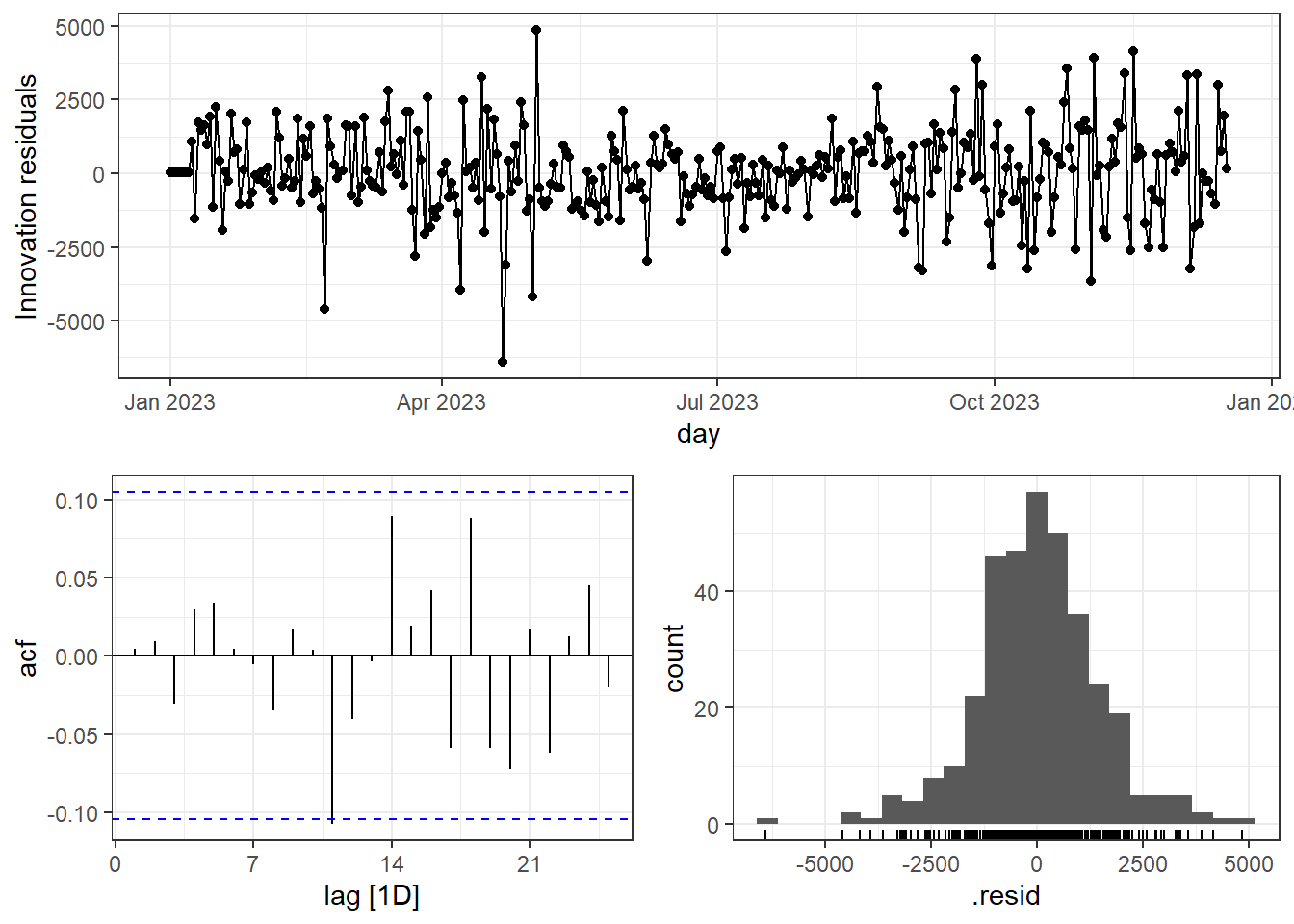
A Figura 7.3 apresenta os gráficos de resíduos para \(\varepsilon_t\). Observa-se independência no tempo e boa aproximação com a normal.
A Tabela 7.1 expõe o resultado do teste de Ljung-Box. O teste deve considerar 6 graus de liberdade, uma vez que o modelo ARIMA apresenta seis coeficientes. O teste confirma ausência de autocorrelação residual.
| Estatística | pvalor |
|---|---|
| 78,08 | 0,15 |
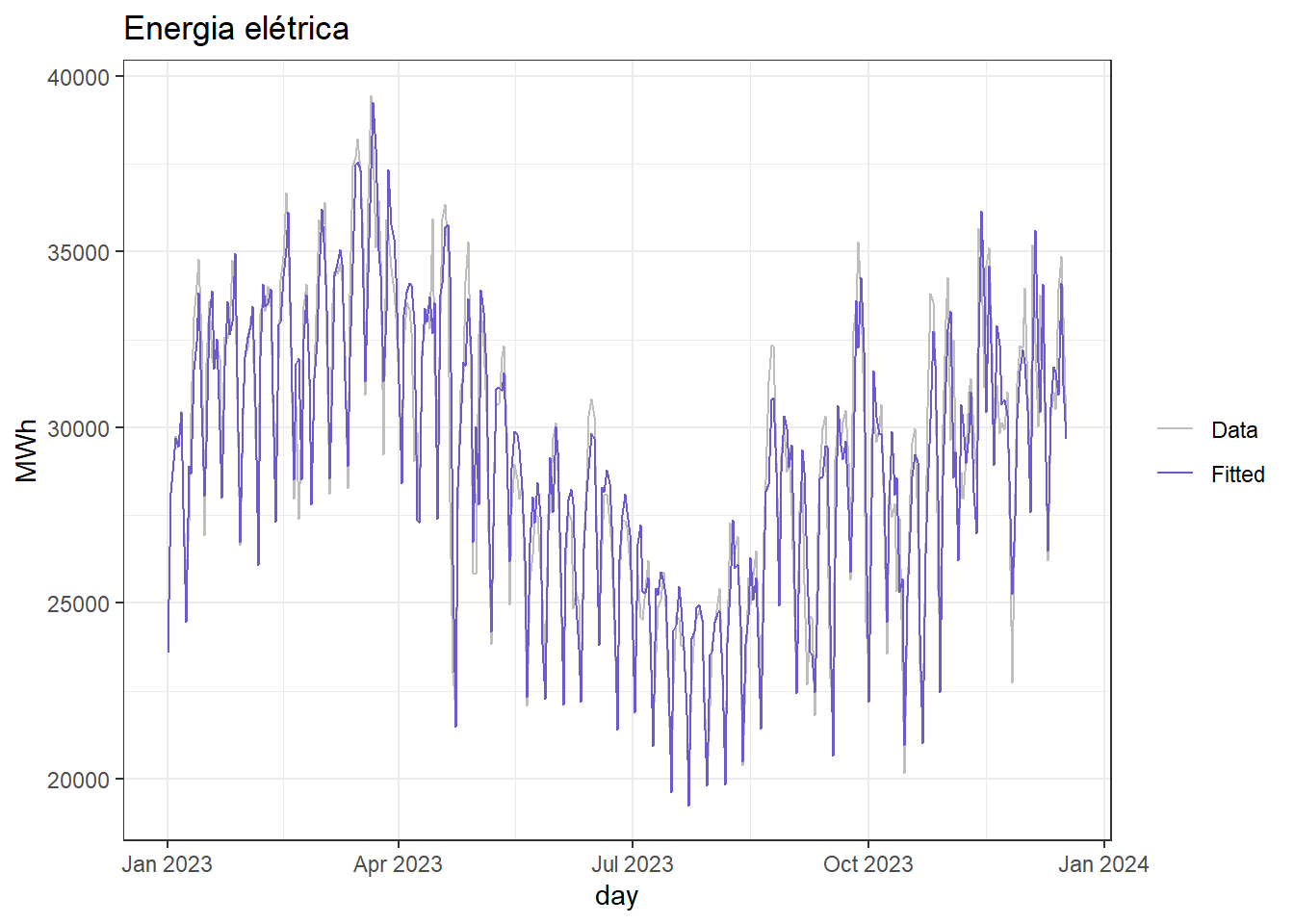
A Figura 7.4 expõe a série ajustada para o consumo de energia hidráulica. Observa-se boa aproximação com a série original.
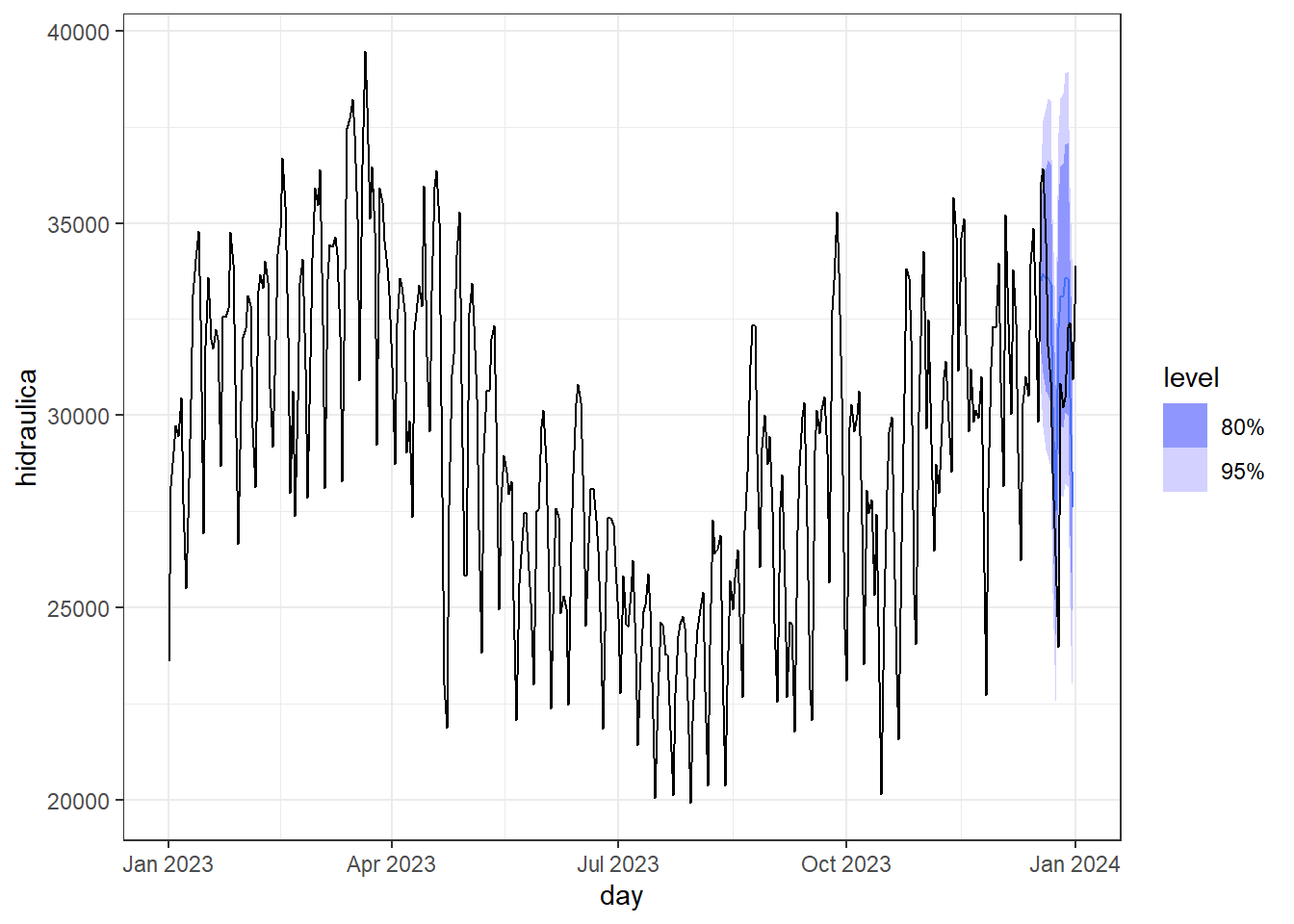
A Figura 7.5 expõe a previsão para as duas últimas semanas do ano para o consumo de energia hidráulica.
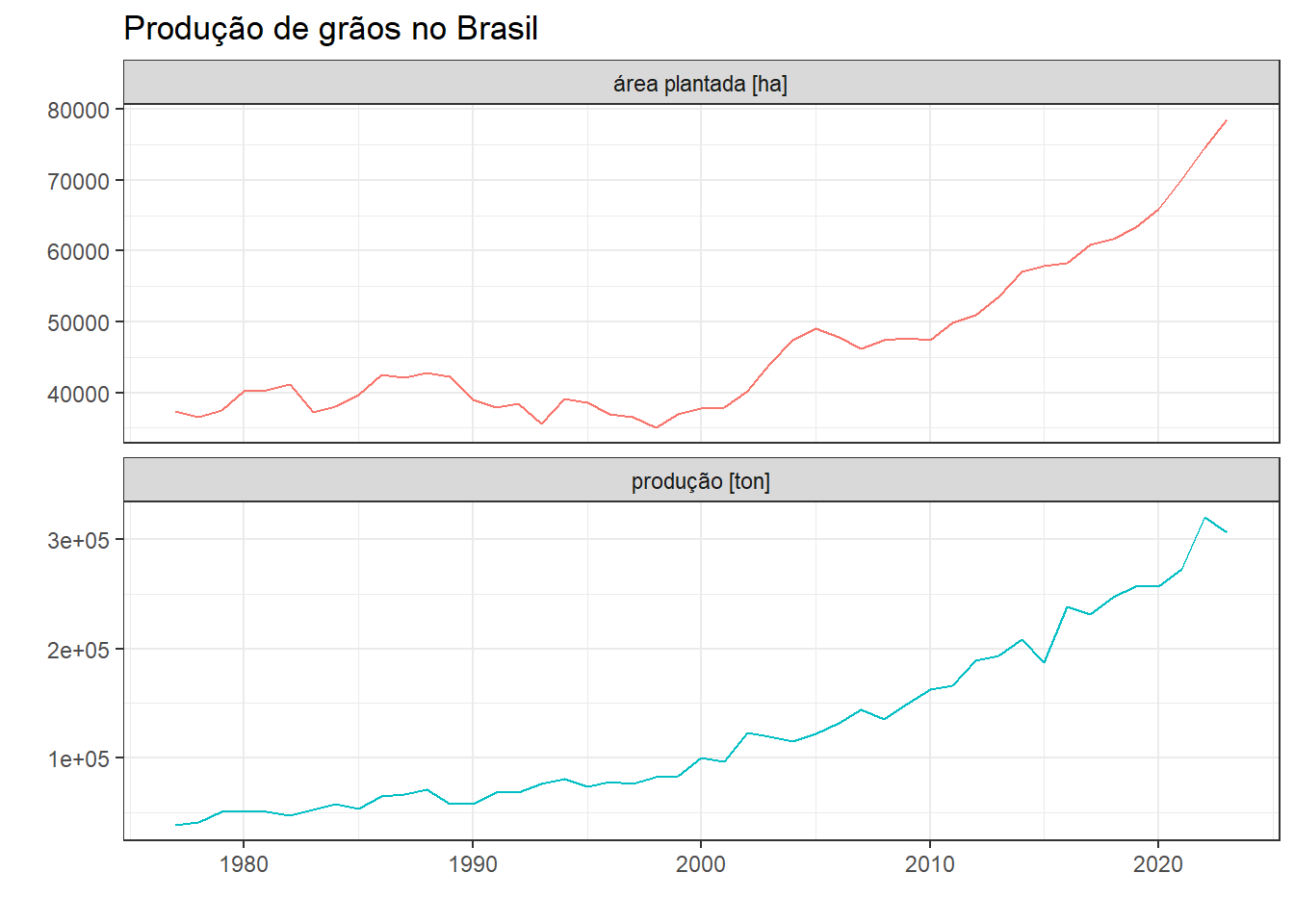
Um outro exemplo adequado à regressão dinâmica seria o de previsão de produção de grãos considerando a área plantada como série regressora. Conforme, visto no capítulo 4, ao se considerar tal caso a regressão apenas não foi suficiente, uma vez que os resíduos apresentavam autocorrelação positiva e significativa até a defasagem de 4 unidades de tempo. A Figura 7.6 plota novamente as séries em questão.
A seguir expõe-se o resultado da modelagem de regressão dinâmica obtido para prever a produção de grãos.
Series: producao
Model: LM w/ ARIMA(1,1,0) errors
Coefficients:
ar1 area_plantada intercept
-0,5777 2,3417 3330,9042
s.e. 0,1248 0,6146 967,0258
sigma^2 estimated as 87293212: log likelihood=-442,22
AIC=892,45 AICc=893,53 BIC=899,4\[ y_t = 3330,90 + 2.34 x_t + \eta_t \\ (1 + 0,58B)(1 - B)\eta_t = \varepsilon_t \]
Ou sem usar o operador de defasagem:
\[ \begin{align} y_t &= 3330,90 + 2.34 x_t + \eta_t \\ \eta'_t &= -0,58\eta'_{t-1} + \varepsilon_t\end{align} \]
A Figura 7.7 plota os resíduos obtidos para o modelo de regressão dinâmica para produção de grãos no Brasil. Os resíduos do modelo autoregressivo devem atender às pressuposições.
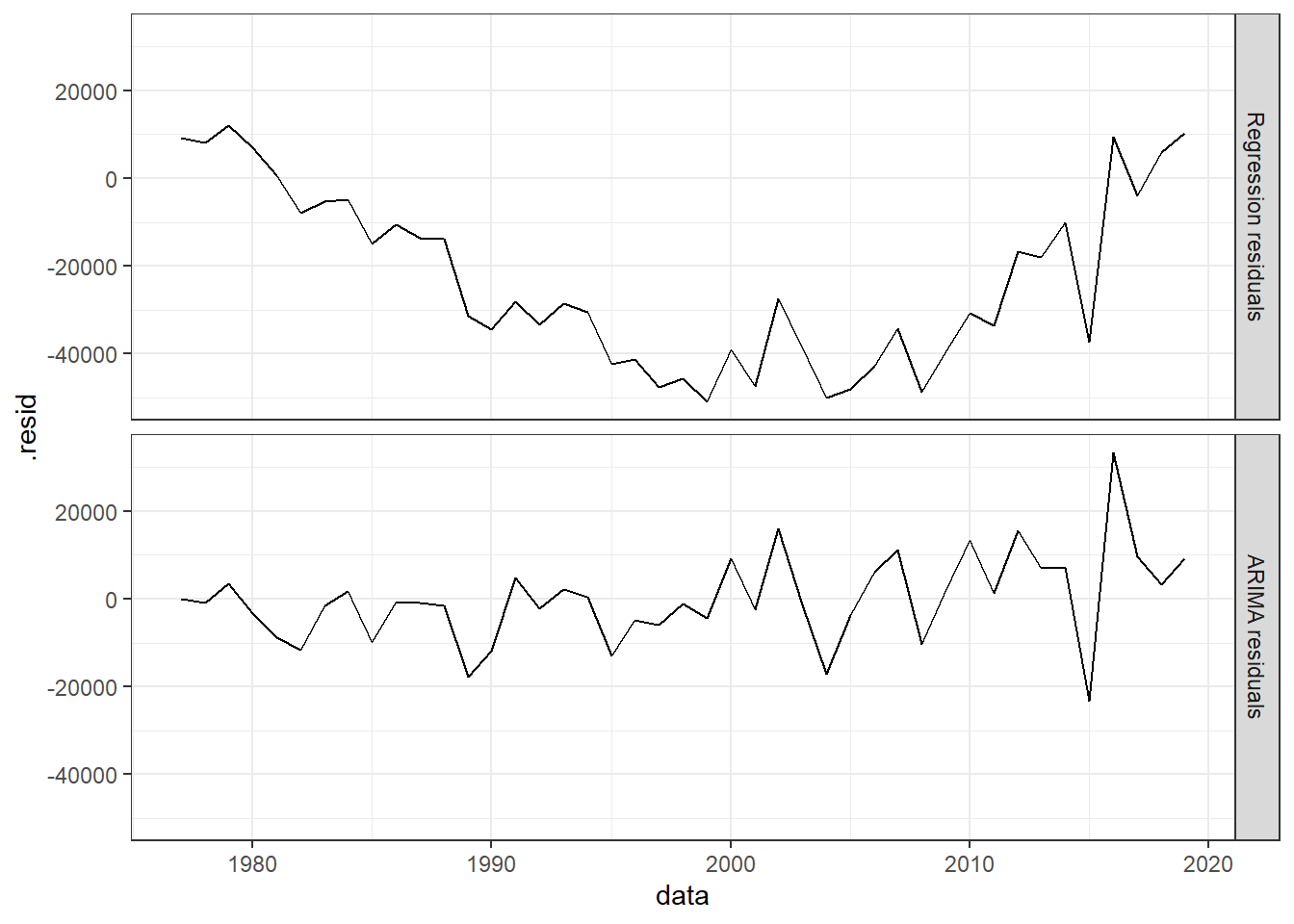
A Figura 7.8 expõe os gráficos dos resíduos do modelo autoregressivo do erro do modelo de regressão para produção de de grãos em função da área plantada. Pode-se observar a ausência de autocorrelação e boa aproximação com a distribuição normal.
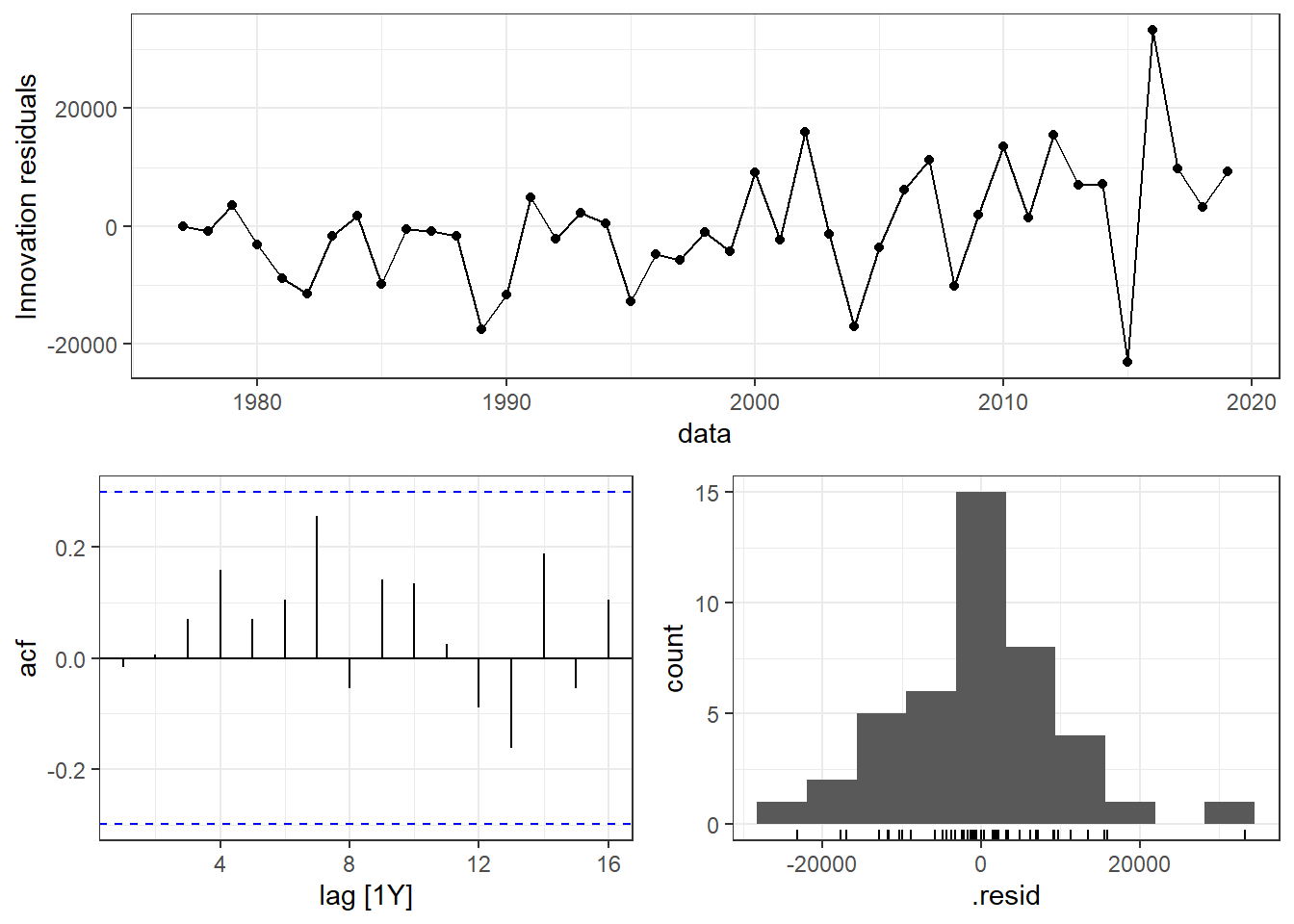
O teste de Ljung-Box, aprensentado na Tabela 7.2, confirma a ausência de autocorrelação residual.
| Estatística | pvalor |
|---|---|
| 7,92 | 0,54 |
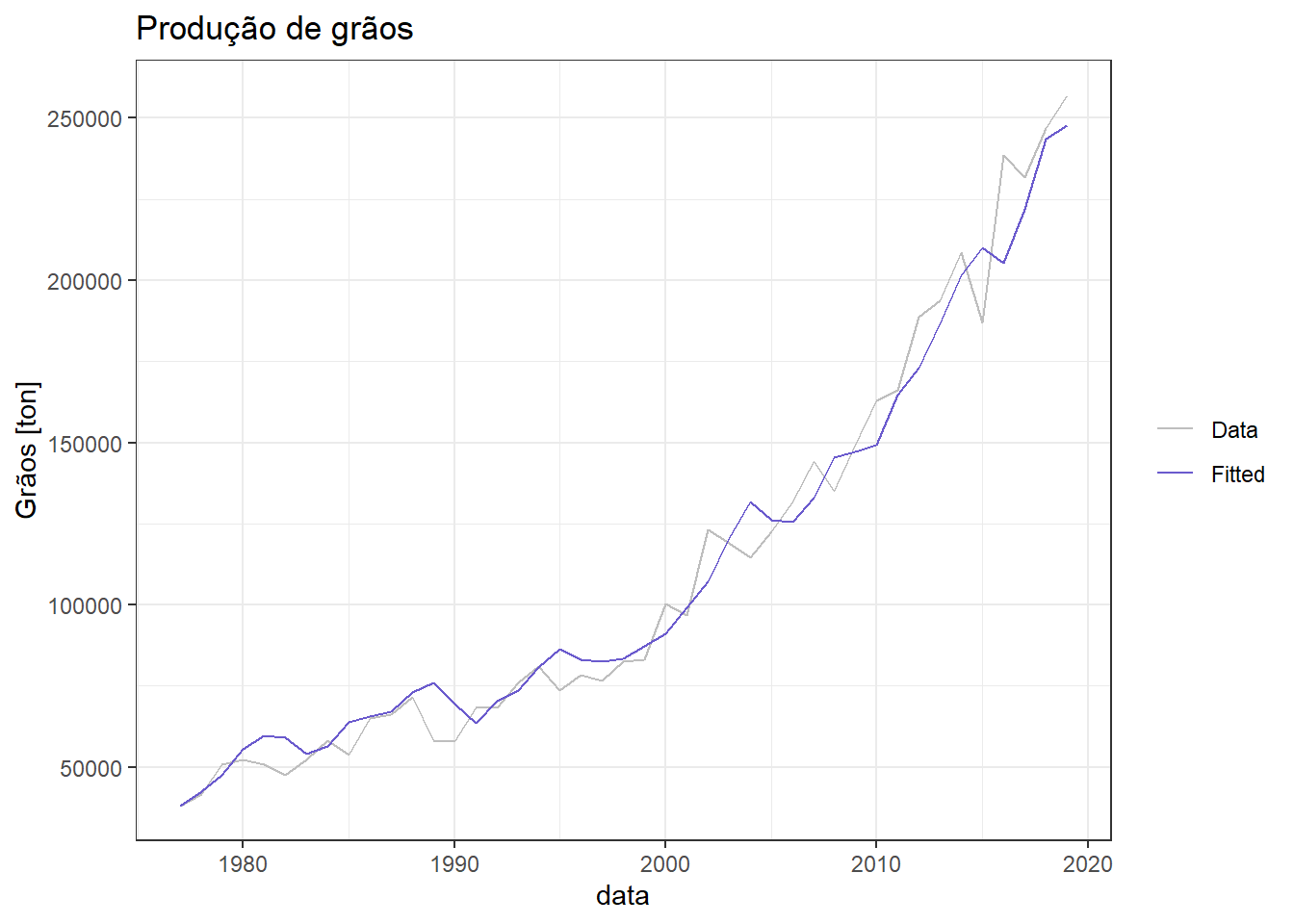
A Figura 7.9 plota os valores ajustados do modelo de regressão dinâmica para produção de grãos em função da área plantada. É interessante comparar tal modelo com o obtido no capítulo 4 onde apenas se considerava um modelo de regressão de séries temporais.
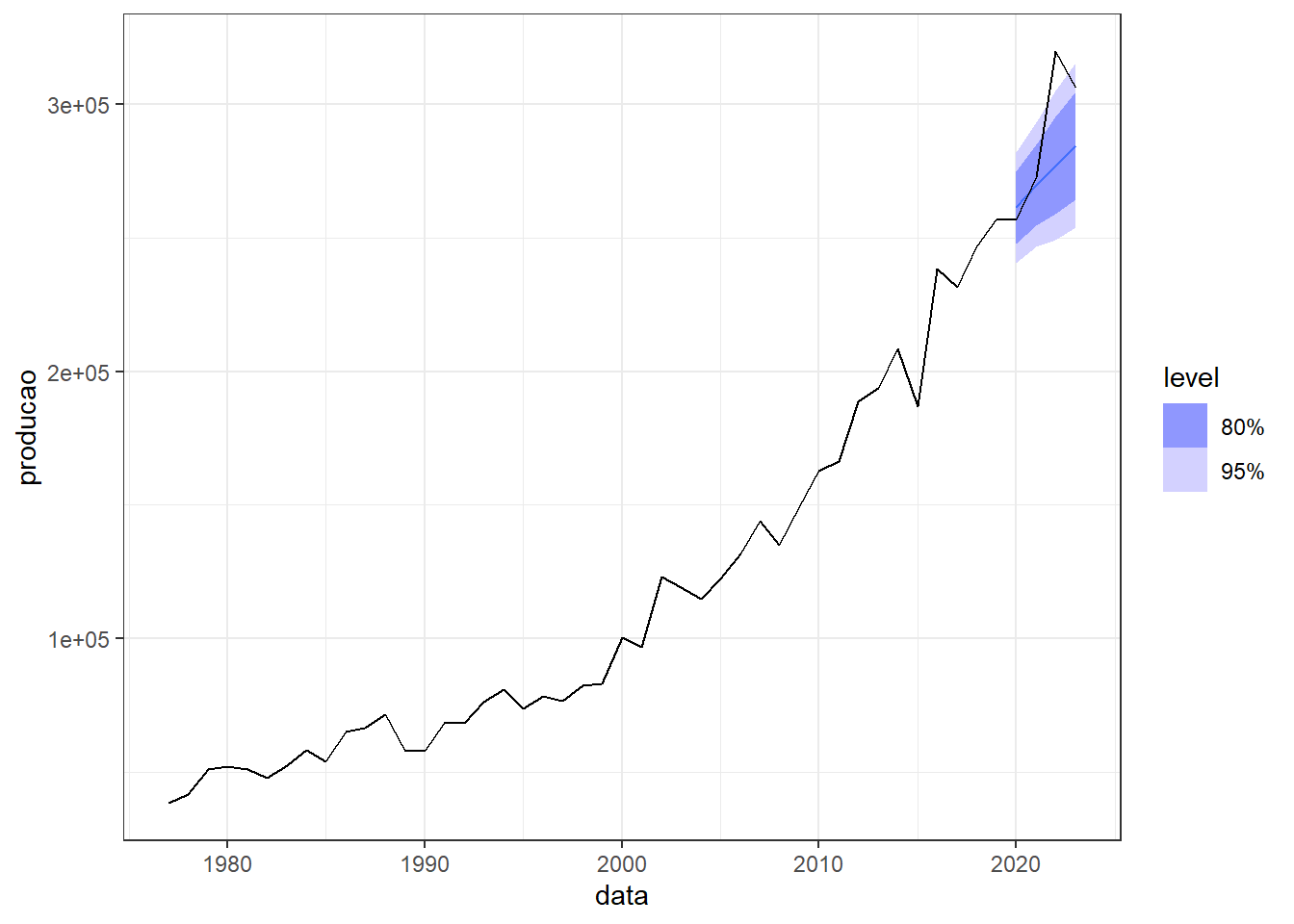
A Figura 7.10 plota a previsão de 2020 a 2023 para o modelo de regressão dinâmica em discussão. É importante alimentar o modelo não somente com o tempo desejado à frente, mas também com dados da variável regressora. Neste caso, foram separados dados dos últimos 4 anos disponíveis para tal. Observa-se que para os dois últimos anos a quantidade produzida superou a quantidade prevista pelo modelo, mesmo com a queda em 2023.
7.1.1 Estimativa de modelos de regressão dinâmica
A estimativa conjunta dos termos de regressão e dos termos do modelo ARIMA para tratar o erro da regressão pode ser realizada via máxima verossimilhança. Para fins de simplificação, seja um modelo de regressão para \(y_t\) em função de uma série exógena ou independente, \(x_t\), com erro descrito por um modelo AR(1), conforme Equação 7.2, com \(\varepsilon_t \sim N(0, \sigma^2)\).
\[ \begin{matrix} y_t = \beta_0 + \beta_1x_{t1} + \eta_t, \\ \eta_t = \phi\eta_{t-1} + \varepsilon_t \end{matrix} \tag{7.2}\]
Logo, \(y_t\) tem média \(\beta_0 + \beta_1x_{t1} + \phi\eta_{t-1}\) e variância \(\sigma^2\). A função densidade de probabilidade conjunta de \(y_1, y_2, \dots, y_t\) pode ser denotada segundo a ?eq-densconj, supondo indep
\[ f(y_1, y_2, \dots, y_t|\beta_0 + \beta_1x_{t1} + \phi\eta_{t-1},\sigma^2) \]
7.2 Modelos com defasagem distribuída
É comum em regressão dinâmica que as séries regressoras tenham efeito na série de interesse com atraso, isto é, a mudança na série regressora, \(x_t\), só será observada na série de interesse, \(y_t\), após alguns períodos. Em diversas aplicações este efeito defasado é esperado e passível de explicação. Por exemplo, um investimento em publicidade no período presente possivelmente não terá reflexo imediato nas vendas, mas sim em um futuro próximo. O efeito de uma política governamental no controle da inflação não terá efeito imediato nos preços e no consumo. No caso da relação entre demanda de energia elétrica e temperatura, pode-se elencar algumas razões para a defasagem entre o consumo de energia e o aumento de temperatura. O efeito do aumento da temperatura no consumo de energia não é instantâneo, pois os edifícios demoram um pouco a esquentar, de forma que a demanda por ar condicionado, por exemplo, seja defasada. As pessoas geralmente estão fora de casa durante a tarde, o horário mais quente do dia e usam o ar condicionado durante a noite. O consumo continua alto mesmo depois de a temperatura começar a cair, uma vez que o calor persiste por horas após a temperatura máxima.
Seja um modelo de regressão dinâmica para \(y_t\) em função de apenas uma variável, \(x_t\), com defasagem distribuída escrito segundo a Equação 7.3, onde \(\eta_t\) é modelado por um processo ARIMA. \(\beta(B)\) é denominada função de transferência ou de resposta de impulso e descreve como \(x_t\) muda \(y_t\) ao longo do tempo.
\[ \begin{align} y_t =& c + \beta_0x_t + \beta_1x_{t-1} + \dots + \beta_kx_{t-k} + \eta_t \\ =& c + (\beta_0 + \beta_1B + \beta_2B^2 + \dots + \beta_kB^k)x_t + \eta_t \\ =& c + \beta(B)x_t + \eta_t \\ \end{align} \tag{7.3}\]
Box et al. (2008) e Pankratz (2012) discutem métodos de identificação de modelos de regressão dinâmica. Aqui sugere-se uma abordagem prática de identificação considerando a função de correlação cruzada (crossed correlation function - CCF) entre \(y_t\) e \(x_t\). Sejam as séries de produção total mensal de veículos automotores, do número de emplacamentos mensal e do consumo de energia mensal da indústria automobilística. As duas primeiras séries estão disponíveis em Anfavea e a terceira está disponível em Empresa de Pesquisa Energética. Tais séries são plotadas na Figura 7.11. Observa-se um padrão similar entre as séries. Observa-se também a queda em todas as séries devido a pandemia.
A Figura 7.12 expõe os gráficos sazonais das séries. Observa-se um padrão sazonal anual, com menor volume de produção e consumo de energia em janeiro e dezembro.
A Tabela 7.3 expõe o resultado do teste de raízes unitárias de KPSS para tais séries. Comprova-se a rejeição da hipótese nula de estacionariedade.
| Série | Estatística | pvalor |
|---|---|---|
| emplacamento | 1,3372506 | 0,0100000 |
| energia | 0,5820566 | 0,0242676 |
| producao | 1,1436241 | 0,0100000 |
A correlação cruzada \(r_{xy,k}\) mede a correlação entre duas séries \(y_t\) e \(x_t\) com defasagem \(k\) entre as séries. Tal estimativa é importante, uma vez que visa mensurar em quais defasagens as séries de interesse se relacionam melhor. Em regressão dinâmica com defasagem distribuída é importante tal identificação, visando a sugestão de possíveis regressores defasados. A Equação 7.4 expõe o cálculo da função de correlação cruzada amostral.
\[ r_{xy,k} = \frac{\sum_{t=k+1}^T (y_t-\bar{y})(x_{t-k}-\bar{x})}{\sqrt {\sum_{t=1}^T (y_t-\bar{y})^2} \sqrt {\sum_{t=1}^T (x_{t-k}-\bar{x})^2}} \tag{7.4}\]
A Figura 7.13 apresenta o correlograma de correlação cruzada entre as séries da indústria automobilística de consumo de energia e produção com dupla diferenciação - simples e sazonal. A diferenciação é recomendada para avaliação da correlação cruzada, de forma a evitar correlações espúrias. Observa-se correlação mais alta entre as séries diferenciadas sem defasagem. Porém, com defasagem de uma observação também há uma correlação significativa entre as séries. Tal correlação pode estar atrelada à não utilização do just-in-time em todas as etapas de produção. Por exemplo, peças estampadas da carroceria podem ficar em estoque dias ou semanas, de forma que, apesar de diariamente muitos veículos serem produzidos, o início da produção de parte da carroceria foi realizada há dias ou semanas.
A Figura 7.14 expõe os diagramas de dispersão com os coeficientes de correlação de Pearson entre a variação dupla da série de energia, \(y''_t\), e a variação dupla da série de produção de veículos sem defasagem, \(x''_t\) e com defasagem de uma observação \(x''_{t-1}\). Confirma-se o observado no correlograma nas duas barras com maior correlação positiva.
Considernado o correlograma da Figura 7.13, podem-se sugerir alguns modelos SARIMAx tentativos. É importante recordar que o erro \(\eta_t\) é modelado por um processo ARIMA. Sugere-se tentar modelos parcimoniosos, isto é, que apresentem um número menor de parâmetros. Para este caso, tentar-se há, inicialmente, um modelo SARIMAx com 2 defasagens, denominado aqui sarimax012:
\[ y_t = \beta_0 + \beta_1 x_t + \beta_2 x_{t-1} + \beta_3 x_{t-2} + \eta_t. \]
Uma outra opção poderia ser um modelo SARIMAx com 1 defasagem, aqui denominado sarimax01:
\[ y_t = \beta_0 + \beta_1 x_t + \beta_2 x_{t-1} + \eta_t. \]
Outro modelo a ser estimado seria o de regressão dinâmica sem defasagem da série independente, aqui denominado sarimax0:
\[ y_t = \beta_0 + \beta_1 x_t + \eta_t. \]
A Tabela 7.4 expõe o resultado das métricas de ajuste para os modelos tentativos. Foram considerados dados de até 2024 para treinar os modelos. Observa-se que o modelo sarimax012 apresentou melhores resultados considerando o AICc, log da máxima verossimilhança e \(\sigma^2\). O modelo SARIMA sem regressor foi o pior, seguido do SARIMAx com o regressor sem defasagem. Em seguida expõe-se o resultado detalhado deste modelo.
| Modelo | sigma2 | log_lik | AIC | AICc | BIC |
|---|---|---|---|---|---|
| sarimax012 | 497462622 | -1748,549 | 3517,098 | 3518,626 | 3547,532 |
| sarimax01 | 506259449 | -1750,511 | 3519,021 | 3520,263 | 3546,412 |
| sarimax0 | 786114284 | -1783,937 | 3583,873 | 3584,860 | 3608,221 |
| sarima | 1330306504 | -1826,493 | 3658,986 | 3659,145 | 3668,116 |
Series: energia
Model: LM w/ ARIMA(2,0,0)(2,0,0)[12] errors
Coefficients:
ar1 ar2 sar1 sar2 producao lag(producao) lag(producao, 2)
0,3849 0,2165 0,2995 0,3529 0,6637 0,5068 -0,1080
s.e. 0,0795 0,0804 0,0785 0,0838 0,0524 0,0542 0,0532
intercept
323913,91
s.e. 19656,05
sigma^2 estimated as 4,86e+08: log likelihood=-1758,82
AIC=3535,63 AICc=3536,87 BIC=3563,08O modelo obtido pode ser expresso na Equação 7.5, com \(\eta\) seguindo um modelo autoregressivo de segunda ordem tanto para a tendência quanto para a sazonalidade, o que consiste em um modelo SARIMA\((2,0,0)(2,0,0)_{12}\). A série não foi diferenciada para modelagem. Pelo modelo, observa-se que não foi necessária, uma vez que \(d=D=0\), de forma que a ausência estacionariedade foi bem capturada pelo regressor. Entretanto, em outros casos onde o regressor não conseguir deixar o erro \(\eta\) sem necessidade de defasagem, sugere-se realizar a modelagem com as séries diferenciadas.
\[ \begin{align} y_t =& 323913{,}91 + 0{,}6637\, x_t + 0{,}5068\, x_{t-1} - 0{,}1080\, x_{t-2} + \eta_t \\ \eta_t =& 0{,}3849 \eta_{t-1} + 0{,}2165 \eta_{t-2} + 0{,}2995 \eta_{t-12} + 0{,}3529 \eta_{t-24} + \varepsilon_t \end{align} \tag{7.5}\]
A Figura 7.15 expõe os gráficos de resíduos do modelo sarimax012. Observa-se Padrão aleatório, normalidade e ausência de autocorrelação, porém um desvio considerável devido à parada na produção dado a pandemia de COVID-19.
Por fim, a Figura 7.16 expõe a previsão para o modelo SARIMAx para os 6 primeiros meses de 2025. Observa-se excelente adequação às observações deste período. Como a previsão para este tipo de modelo depende da série regressora, neste caso a série de produção de veículos, pode-se trabalhar a previsão com cenários, conforme visto no capítulo 4. Uma proposta interessante para o caso do consumo de energia, seria trabalhar os cenários de produção considerando dados de planejamento da produção ou então aproximar via ARIMA ou outro método a série de produção e usar as previsões como cenários para o modelo SARIMAx. O exemplo proposto possibilitaria à indústria estimar a demanda energética a partir do planejamento da produção. Obviamente, estes dados são de estatísticas nacionais, mas, possivelmente, as séries específicas das montadoras nacionais apresentam padrões similares, viabilizando o emprego de tal abordagem.
Na regressão dinâmica também é possível adicionar regressores binários (dummy). Para o exemplo da previsão do consumo de energia em função da produção de veículos com defasagem, pode-se observar pelas Figura 7.11 e Figura 7.12 e, também, pelos resíduos do melhor modelo na Figura 7.15, que, nos meses abril a junho de 2020, a produção e o consumo de energia foram baixíssimos, especialmente em abril, quando a produção parou devido à Pandemia de COVID19. A Tabela 7.5 apresenta o resultado do modelo sarimax012 com e sem a variável dummy definida conforme segue. Observa-se que o modelo com tal variável, sarimax012dummy, apresentou melhor ajuste.
\[ x_{t,\text{dummy}} = \begin{cases} 1, & \text{se } t \in \{\text{04 a 06/2020}\} \\ 0, & \text{caso contrário} \end{cases} \]
| Modelo | sigma2 | log_lik | AIC | AICc | BIC |
|---|---|---|---|---|---|
| sarimax012 | 485975762 | -1758,817 | 3535,634 | 3536,867 | 3563,083 |
| sarimax012dummy | 402499522 | -1744,087 | 3510,173 | 3512,007 | 3543,722 |
A Figura 7.17 apresenta os gráficos de resíduos para o modelo sarimax012dummy. O tratamento da parada da produção devido a pandemia de COVID-19 com uma variável binária apresentou eficácia na redução do valor discrepante observado nos resíduos do modelo sarimax. Finalmente, a Tabela 7.6 apresenta o resultado do teste de Ljung-Box para ambos os modelos, indicando ausência de autocorrelação residual.
| Modelo | Estatística | pvalor |
|---|---|---|
| sarimax012 | 20,90 | 0,40 |
| sarimax012dummy | 16,54 | 0,68 |
A Figura 7.18 apresenta a previsão para primeiro semestre de 2025 para os modelos sarimax012 e sarimax012dummy. Para o modelo com a variável binária, é importante definir os valores desta, no caso \(x_{t,dummy} = 0\), uma vez que não houve pandemia no período.
7.3 Regressão dinâmica harmônica
Uma possibilidade para casos com frequência horária ou menor, a regressão dinâmica harmônica considera termos estimados via série de Fourier. Modelos ARIMA e ETS tradicionais foram concebidos para considerar um número limitado de estações ou períodos sazonais, por exemplo, \(m=12\) para séries anuais e \(m=4\) para trimestrais. A regressão dinâmica harmônica é viável para séries longas, podendo aproximar séries que incluam simultaneamente sazonalidade de frequências dinstintas.
Os dados de demanda de eletricidade do sudeste e centro oeste do Brasil anteriormente considerados na regressão dinâmica em função da temperatura foram considerados em frequência diária, sendo tomada a média do consumo em função da temperatura média. É possível trabalhar a mesma série disponível em frequência horária usando regressão dinâmica com termos de Fourier.
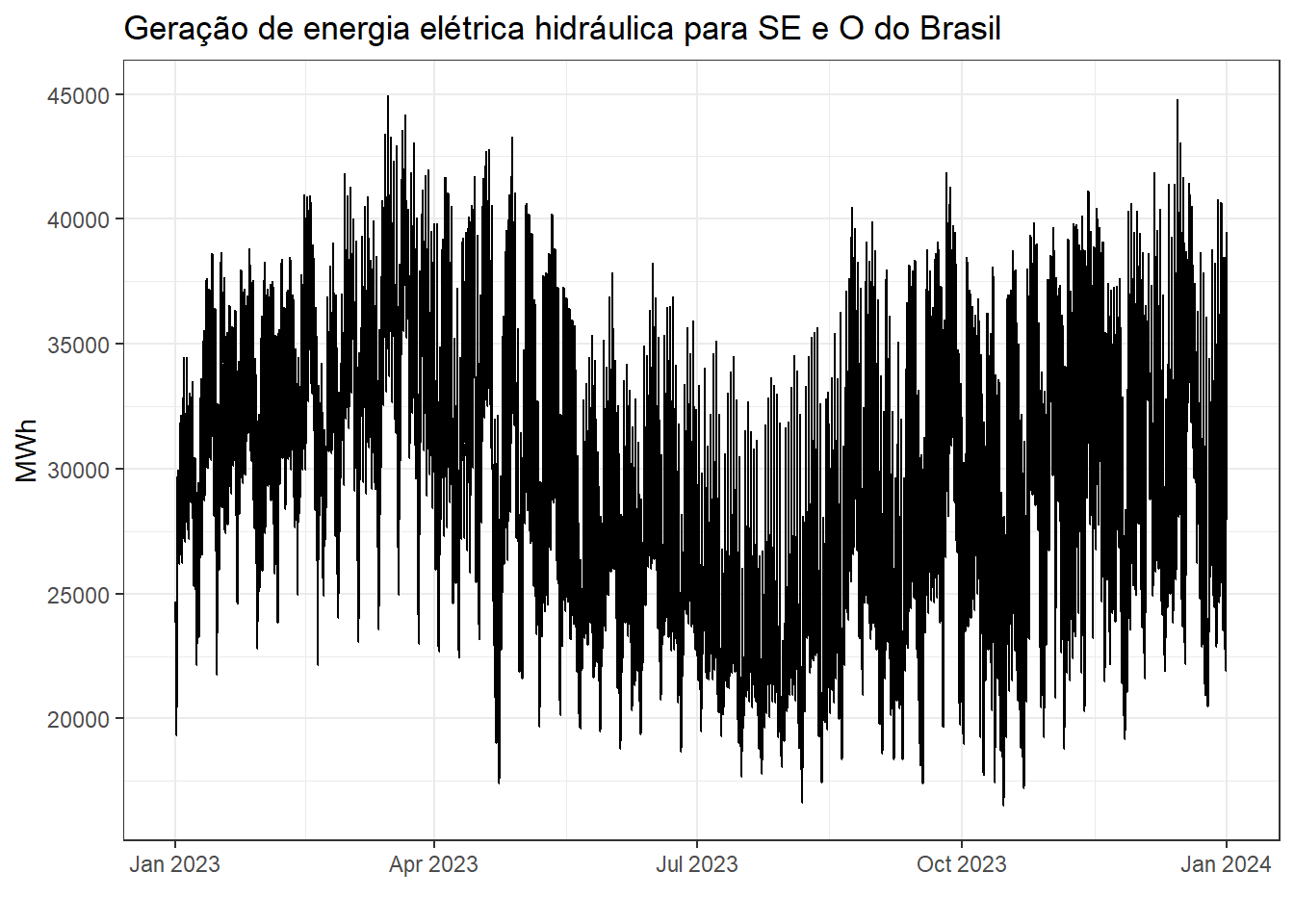
A Figura 7.19 expõe a série temporal de geração de energia hidráulica para o sudeste e centro oeste do Brasil no ano de 2023 com frequência horária. Tal série apresenta 8760 observações.
A Figura 7.20 expõe o gráfico de sazonalidade diária para as séries de consumo de energia elétrica hidráulica e de temperatura para o sudeste e centro oeste do Brasil. Observa-se ciclos muito similares para ambas as séries, com mínima pela manhã e máxima a tarde. Já a Figura 7.21 expõe outro gráfico sazonal com cada mês em um painel. É possível notar a sazonalidade diária, além da tendência da temperatura e do consumo de energia segundo as estações do ano.
A Tabela 7.7 expõe os resultados de ajuste de seis modelos de regressão dinâmica harmônica para a série de demanda de eletricidade do sudeste e centro oeste do Brasil considerando de 1 a 6 termos de Fourier. Observa-se que a adição de mais termos melhora o ajuste do modelo.
| .model | sigma2 | log_lik | AIC | AICc | BIC |
|---|---|---|---|---|---|
| K = 1 | 0,0009581 | 14167,48 | -28316,96 | -28316,94 | -28255,42 |
| K = 2 | 0,0007851 | 14853,98 | -29687,96 | -29687,93 | -29619,59 |
| K = 3 | 0,0007842 | 14858,91 | -29693,83 | -29693,78 | -29611,78 |
| K = 4 | 0,0007631 | 14953,72 | -29879,44 | -29879,38 | -29783,72 |
| K = 5 | 0,0007624 | 14958,10 | -29884,21 | -29884,13 | -29774,81 |
| K = 6 | 0,0006653 | 15428,40 | -30818,80 | -30818,69 | -30688,89 |
A Figura 7.22 plota a previsão uma semana a frente para os modelos obtidos. Os dados foram plotados de Setembro em diante para facilitar a visualização.
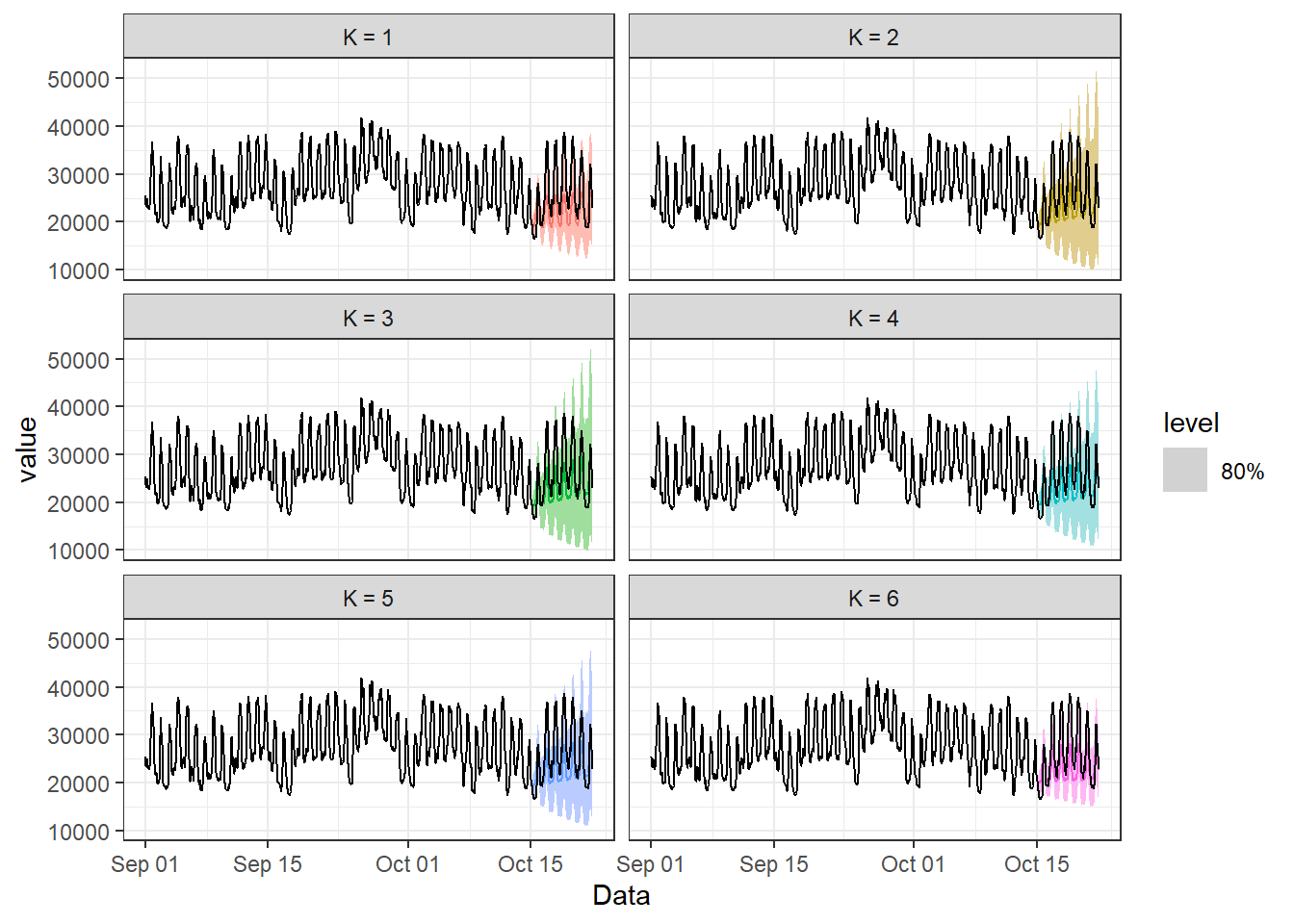
A Tabela 7.8 plota o desempenho obtido para a previsão uma semana a frente considerando os modelos de regressão dinâmica harmônica. Observa-se que o modelo com “K = 3” termos apresentou melhor resultado.
| .model | RMSE | MAE | MAPE |
|---|---|---|---|
| K = 1 | 8424,605 | 7295,301 | 15,57196 |
| K = 2 | 6511,291 | 5433,725 | 12,57678 |
| K = 3 | 6520,130 | 5441,139 | 12,58419 |
| K = 4 | 6534,698 | 5499,981 | 12,62594 |
| K = 5 | 6547,457 | 5513,284 | 12,63231 |
| K = 6 | 6512,690 | 5468,527 | 12,59147 |