5  Suavização exponencial

5.1 Suavização exponencial simples

A suavização exponencial consiste em uma média ponderada das observações anteriores, com peso decaindo exponencialmente à medida que as observações ficam mais distantes no tempo.

O caso simples pode ser descrito matematicamente conforme segue:

\[ \hat y_{T+1|T} = \alpha y_T + \alpha(1-\alpha)y_{T-1} + \alpha(1-\alpha)^2y_{T-2}+... \]

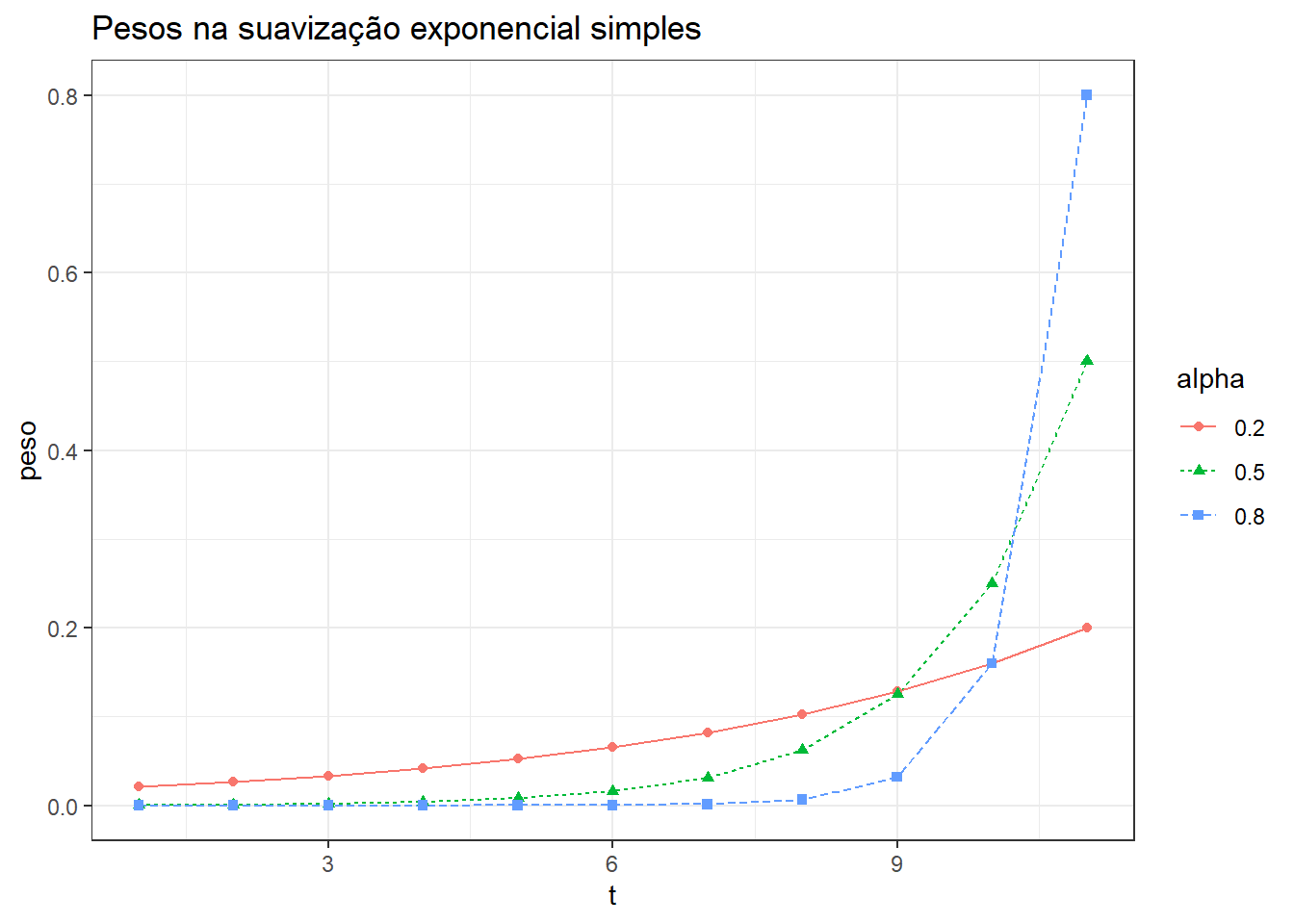
onde \(0< \alpha <1\) consiste no parâmetro de suavização. A previsão um passo à frente consiste em uma média ponderada das observações anteriores, \(y_1,...,y_T\), com taxa de decrescimento dos pesos controlada pelo parâmetro \(\alpha\). A Tabela 5.1 expõe os pesos para cinco últimas observações da série para distintos valores de \(\alpha\). Observa-se que a soma dos pesos é próxima de 1.

Tabela 5.1: Pesos na suavização exponencial simples

Observação	\(\alpha=0.2\)	\(\alpha=0.5\)	\(\alpha=0.8\)
\(y_T\)	0.200000	0.500000	0.800000
\(y_{T-1}\)	0.160000	0.250000	0.160000
\(y_{T-2}\)	0.128000	0.125000	0.032000
\(y_{T-3}\)	0.102400	0.062500	0.006400
\(y_{T-4}\)	0.081920	0.031250	0.001280
\(y_{T-5}\)	0.065536	0.015625	0.000256

A Figura 5.1 expõe os mesmos pesos plotados segundo o tempo. Observa-se que quanto maior o \(\alpha\), maior a taxa de decrescimento dos pesos da última observação em relação às anteriores.

Figura 5.1: Pesos na suavização exponencial simples

O modelo exposto para prever a observação futura pode ser descrito sempre considerando a última observação e a previsão desta:

\[ \hat y_{T+1|T} = \alpha y_T +(1-\alpha)\hat y_{T|T-1} \]

De forma similar os valores estimados para a série ficam:

\[ \hat y_{t+1|t} = \alpha y_t +(1-\alpha)\hat y_{t|t-1}, \]

para \(t=1,...,T\).

Seja \(l_0\) o valor estimado para a primeira observação, \(t=1\), então:

\[ \begin{align} \hat y_{2|1} &= \alpha y_1 +(1-\alpha) l_0 \\ \hat y_{3|2} &= \alpha y_2 +(1-\alpha) \hat y_{2|1} \\ \hat y_{4|3} &= \alpha y_3 +(1-\alpha) \hat y_{3|2} \\ \vdots \\ \hat y_{T|T-1} &= \alpha y_{T-1} +(1-\alpha) \hat y_{T-1|T-2} \\ \hat y_{T+1|T} &= \alpha y_{T} +(1-\alpha) \hat y_{T|T-1} \\ \end{align} \]

Observe que cada equação pode ser substituída na posterior:

\[ \begin{align} \hat y_{3|2} &= \alpha y_2 +(1-\alpha) [\alpha y_1 +(1-\alpha) l_0] \\ &= \alpha y_2 + \alpha(1-\alpha)y_1 +(1-\alpha)^2 l_0\\ \hat y_{4|3} &= \alpha y_3 +(1-\alpha)[\alpha y_2 + \alpha(1-\alpha y_1 +(1-\alpha)^2 l_0] \\ &= \alpha y_3 +\alpha(1-\alpha) y_2 +\alpha(1-\alpha)^2 y_1 +(1-\alpha)^3 l_0 \\ \vdots \\ \hat y_{T+1|T} &= \sum_{j=0}^{T-1} \alpha (1-\alpha)^j y_{T-j}+ (1-\alpha)^T l_0 \\ \end{align} \]

Como o último termo fica muito pequeno para \(T\) grande, então a equação fica conforme o modelo apresentado inicialmente.

A representação em componentes também é comum para a suavização exponencial, sendo o caso simples conforme segue:

\[ \begin{align} \text{Equação de previsão: } \hat y_{t+h} &= l_t\\ \text{Equação de suavização: } l_t &= \alpha y_t + (1-\alpha)l_{t-1},\\ \end{align} \]

onde \(l_t\) consiste no nível no período \(t\) e \(\hat y_{t+h} = l_t\) a previsão no período \(t+h\).

Se \(h=1\), tem-se o valor estimado, enquanto se \(t=T\), tem-se a previsão para além dos dados de treino. Fazendo \(l_t = \hat y_{t+1|t}\) e \(l_{t-1} = \hat y_{t|t-1}\), tem-se o modelo ponderado já exposto. Tal representação não é tão útil para o caso simples, porém, quando considerados termos de tendência e suavização, será. O modelo simples, até aqui explicitado é recomendado para casos sem tendência e sazonalidade.

A Figura 5.2 expõe o resultado da suavização exponencial simples para a série do IPCA no Brasil a partir de 2019. Os parâmetros estimados \(\alpha\) e \(l_0\) expostos na Tabela 5.2 foram estimados minimizando a soma dos quadrados dos erros para as estimativas um passo à frente.

Tabela 5.2: Parâmetros de suavização exponencial simples para a série do IPCA no Brasil a partir de 2019

term	estimate
alpha	0.6356607
l[0]	0.3857116

Figura 5.2: Exponencial simples para a série IPCA no Brasil a partir de 2019

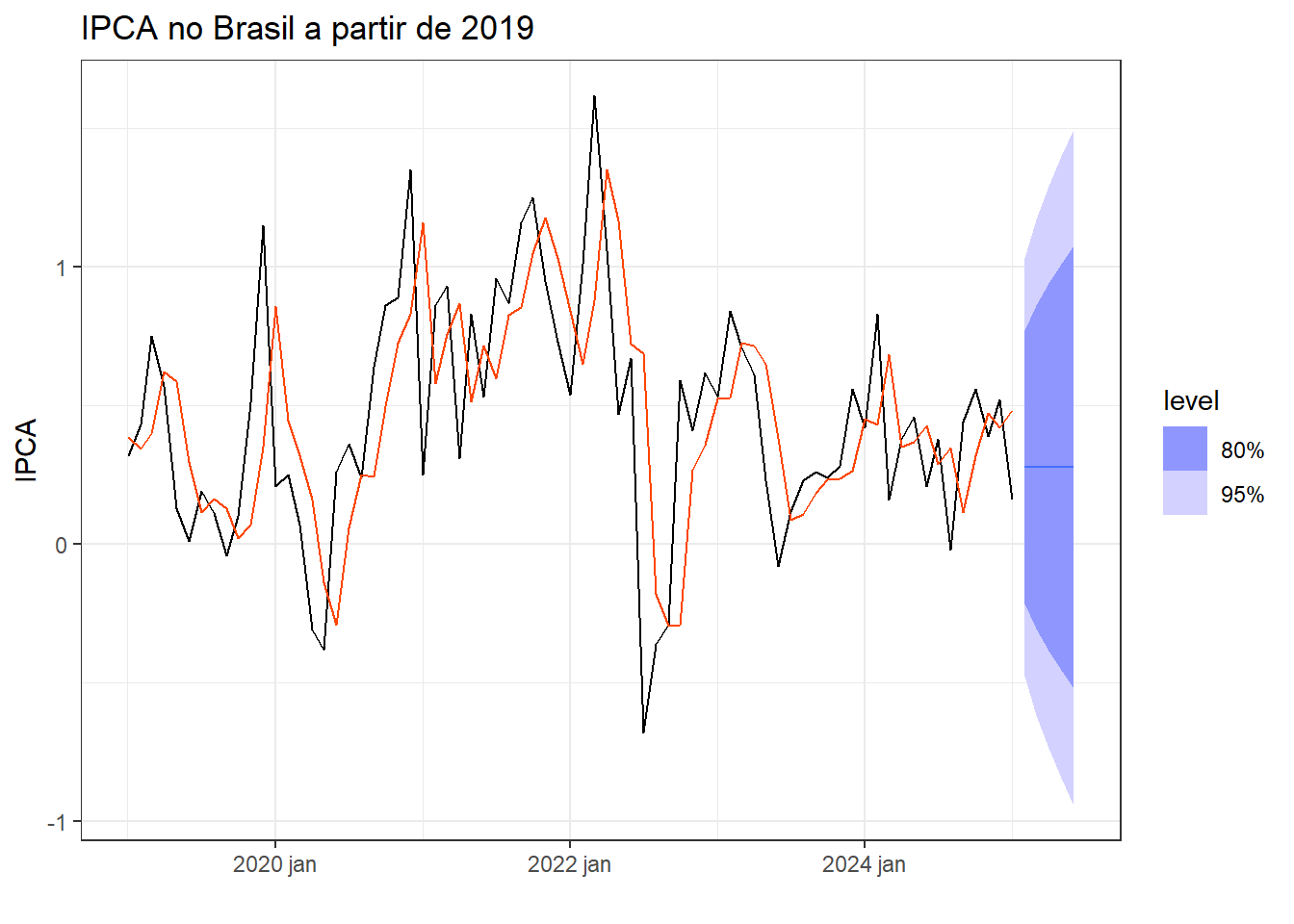
A Tabela 5.3 apresenta os valores estimados \(\hat y_t\) para as últimas observações da série.

Tabela 5.3: Pesos na suavização exponencial simples

index	value	.fitted
2024 ago	-0.02	0.3468724
2024 set	0.44	0.1136660
2024 out	0.56	0.3211037
2024 nov	0.39	0.4729607
2024 dez	0.52	0.4202258
2025 jan	0.16	0.4836484

5.2 Suavização exponencial com tendência

Em casos com tendência pode-se considerar o método de Holt (2004), o qual considera uma equação para o nível, \(l_t\), uma para a tendência, \(b_t\), e a de previsão, \(\hat y_{t+h|t}\).

\[ \begin{align} \text{Equação de previsão: } \hat y_{t+h} &= l_t + hb_t\\ \text{Equação do nível: } l_t &= \alpha y_t + (1-\alpha)(l_{t-1}+b_{t-1})\\ \text{Equação de tendência: } b_t &= \beta^*(l_t-l_{t-1})+(1-\beta^*)b_{t-1} \end{align} \]

Neste caso \(l_t\) é uma média ponderada da observação \(y_t\) e da previsão um passo a frente, dada por \(l_{t-1}+b_{t-1}\). A equação de tendência mostra que \(b_t\) é uma média ponderada da tendência no tempo \(t\), baseada em \(l_t-l_{t-1}\), e na estimativa anterior da tendência, \(b_{t-1}\).

A Figura 5.3 expõe a série anual da população projetada para o Brasil até 2010, revisada em 2008, disponível em IBGE. Observa-se tendência de crescimento muito próxima de linear.

Figura 5.3: População do Brasil

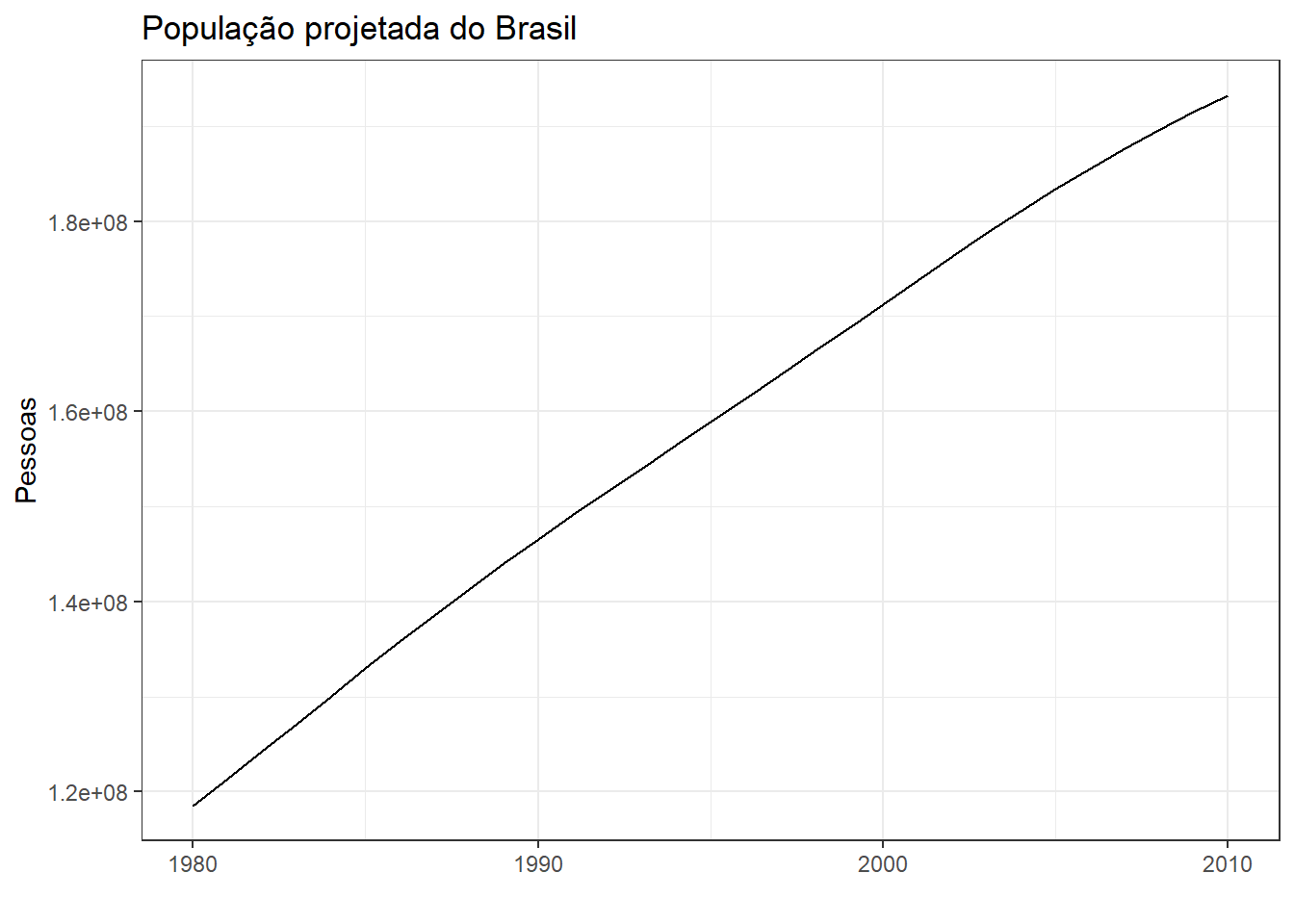
A Tabela 5.4 expõe os parâmetros estimados de suavização exponencial com tendência para a série da populaçao projetada do Brasil.

Tabela 5.4: Parâmetros de suavização exponencial com tendência para a série da população projetada do Brasil

.model	term	estimate
AAN	alpha	9.953798e-01
AAN	beta	4.433299e-01
AAN	l[0]	1.169488e+08
AAN	b[0]	2.842713e+06

5.2.1 Suavização exponencial com tendência amortecida

Um problema do método de Holt (2004) para suavização exponencial com tendência é que ele costuma apresentar uma estimativa linear que em longos horizontes de previsão costuma não se confirmar. Uma opção é a abordagem de Gardner e Mckenzie (1985) que propõe amortecer as previsões. O método inclui o parâmetro de amortecimento \(0<\phi<1\).

\[ \begin{align} \text{Equação de previsão: } \hat y_{t+h} &= l_t + (\phi+\phi^2+...+\phi^h)b_t\\ \text{Equação do nível: } l_t &= \alpha y_t + (1-\alpha)(l_{t-1}+\phi b_{t-1})\\ \text{Equação de tendência: } b_t &= \beta^*(l_t-l_{t-1})+(1-\beta^*)\phi b_{t-1} \end{align} \]

Caso \(\phi=1\), então tem-se o método de Holt já exposto. O método tende a gerar previsões com tendência para curtos períodos e previsões constantes em longos horizontes à frente das observações. A Figura 5.4 expõe as previsões 15 anos à frente para a população do Brasil considerando os dados projetados até 2010. Observa-se que o método de Holt projetaria 212 milhões de pessoas em 2020, enquanto o mesmo amortecido projetaria 204 milhões para o mesmo ano. Foi considerado neste caso \(\phi=0.9\). Dados já observados do censo de 2022 indicam que a população do Brasil neste ano atingiu 203 milhões de pessoas.

Figura 5.4: População do Brasil

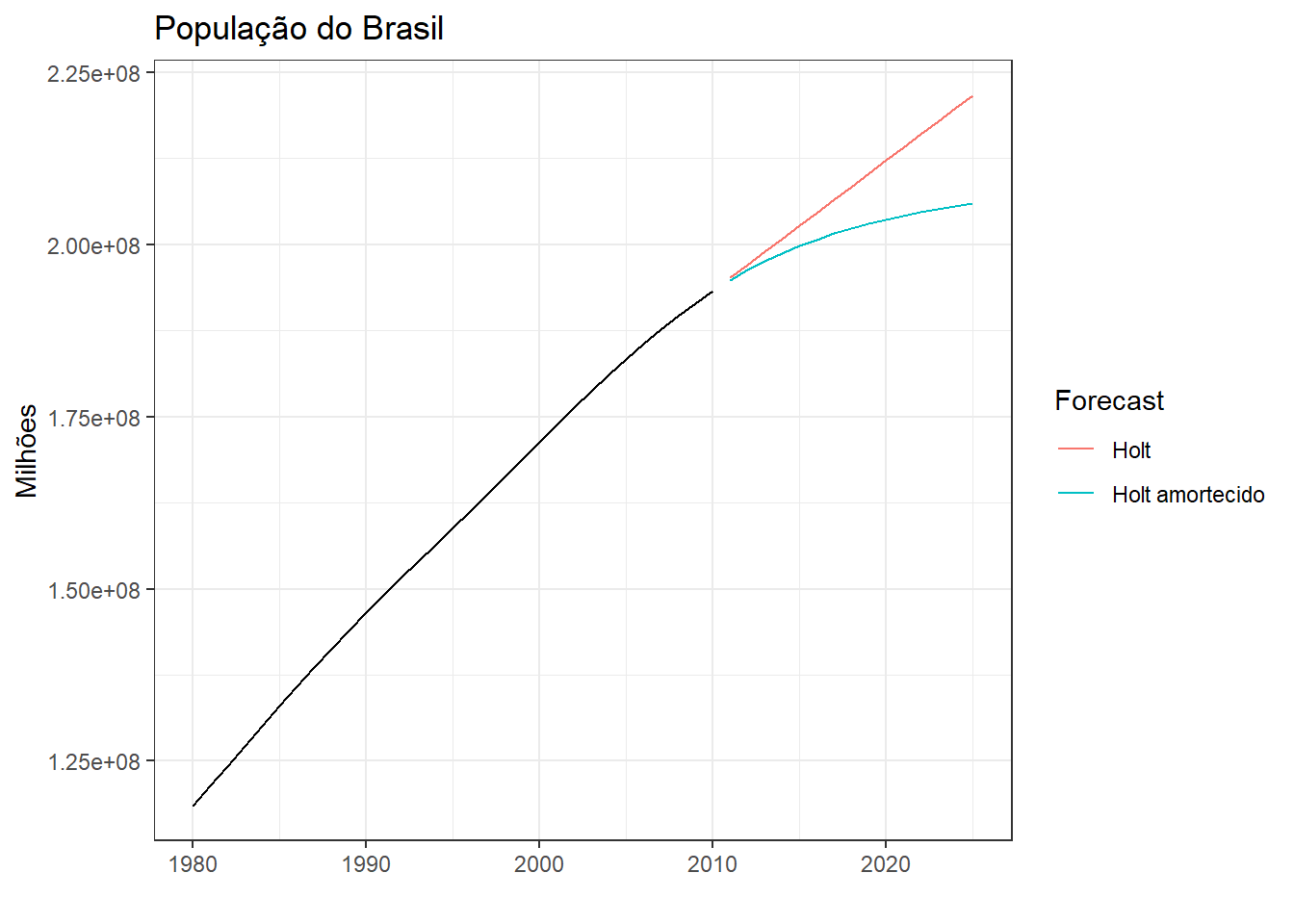
A Figura 5.5 expõe os mesmos métodos aplicados à série anual de emissão de gases de efeito estufa pela indústria, disponível em Sistema de Estimativa de Emissão de Gases. Foi considerado um \(\phi = 0.95\) para o caso com amortecimento.

Figura 5.5: Emissões de gases de efeito estufa pela indústria

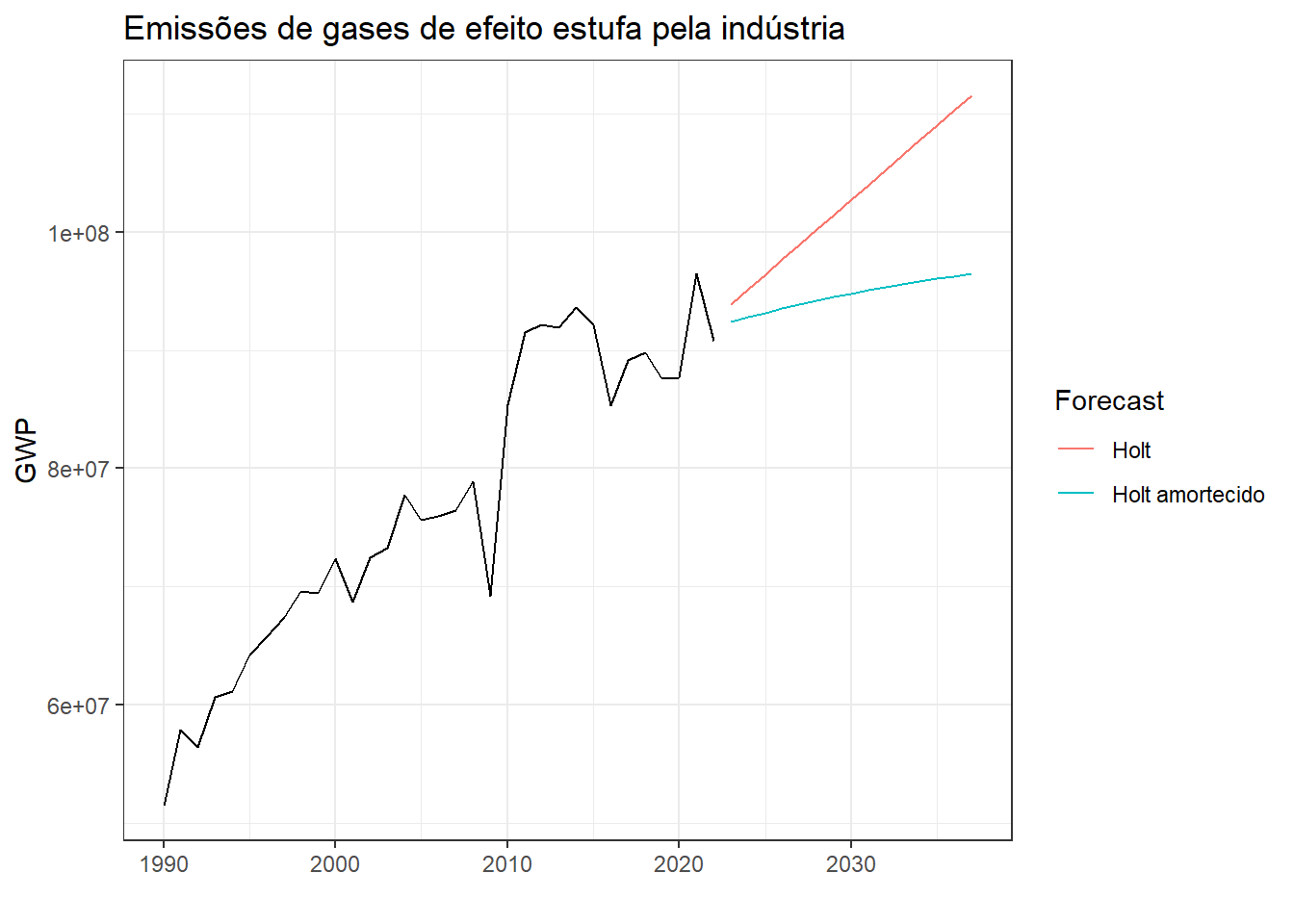
5.3 Suavização exponencial com sazonalidade

Holt (2004) e Winters (1960) consideraram a sazonalidade na suavização exponencial. Logo, além das equações de previsão, nível e tendência, o método inclui uma equação adicional para a sazonalidade. O método considera ambos os casos aditivo e multiplicativo.

O método Holt-Winters aditivo compreende as equações à seguir:

\[ \begin{align} \text{Equação de previsão: } \hat y_{t+h} &= l_t + hb_t + s_{t+h-m(k+1)}\\ \text{Equação do nível: } l_t &= \alpha (y_t-s_{t-m}) + (1-\alpha)(l_{t-1}+b_{t-1})\\ \text{Equação de tendência: } b_t &= \beta^*(l_t-l_{t-1})+(1-\beta^*)b_{t-1}\\ \text{Equação de sazonalidade: } s_t &= \gamma(y_t-l_{t-1}-b_{t-1})+(1-\gamma)s_{t-1}, \end{align} \]

onde \(k\) consiste na parte inteira de \((h−1)/m\) que garante que a estimativa dos índices sazonais usados para previsão vêm do último período sazonal da série. A equação de nível consiste em uma média ponderada entre a observação ajustada sazonalmente, \(y_t-s_{t-m}\), e a previsão não sazonal, \(l_{t-1}+b_{t-1}\), para o tempo \(t\). A equação de tendência não muda e a sazonal considera uma média móvel do índice sazonal atual, \(y_t-l_{t-1}-b_{t-1}\), e do mesmo período da estação anterior, \(s_{t-1}\).

O caso multiplicativo é exposto à seguir.

\[ \begin{align} \text{Equação de previsão: } \hat y_{t+h} &= (l_t + hb_t) s_{t+h-m(k+1)}\\ \text{Equação do nível: } l_t &= \alpha \frac{y_t}{s_{t-m}} + (1-\alpha)(l_{t-1}+b_{t-1})\\ \text{Equação de tendência: } b_t &= \beta^*(l_t-l_{t-1})+(1-\beta^*)b_{t-1}\\ \text{Equação de sazonalidade: } s_t &= \gamma \frac {y_t}{(l_{t-1}-b_{t-1})}+(1-\gamma)s_{t-1}, \end{align} \]

A Figura 5.6 plota a série temporal de exportações do Brasil em US$ FOB, disponível em Resultados do Comércio Exterior Brasileiro - Dados Consolidados. Observa-se em geral tendência de crescimento com estagnação de 2016 a 2021 devido a crise político-econômica e a pandemia.

Figura 5.6: Exportações do Brasil

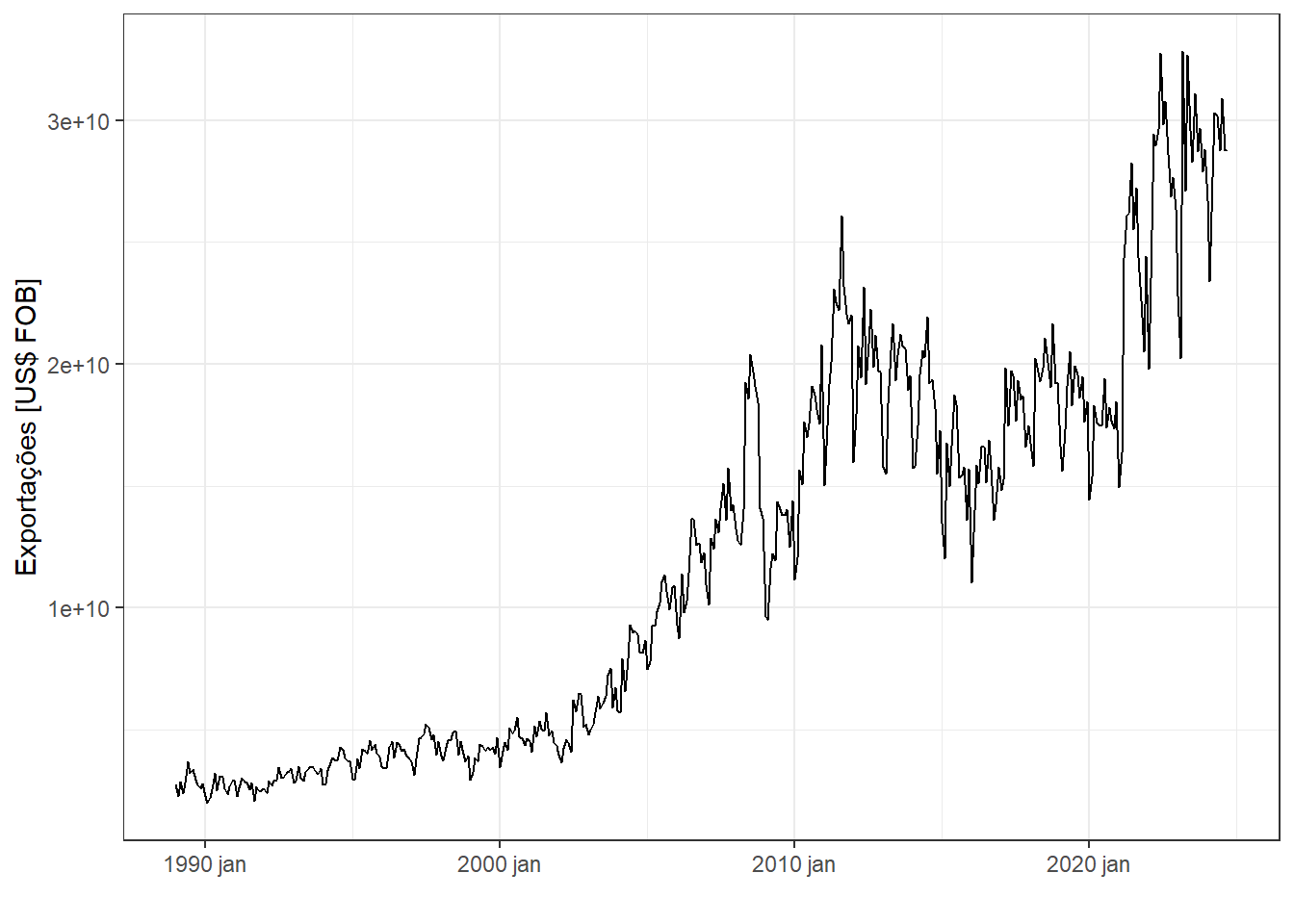
A Figura 5.7 expõe o gráfico sazonal da mesma série. O padrão cíclico não é tão claro, mas nota-se maior volume de exportações de março a agosto.

Figura 5.7: Gráfico sazonal para a série de exportações do Brasil

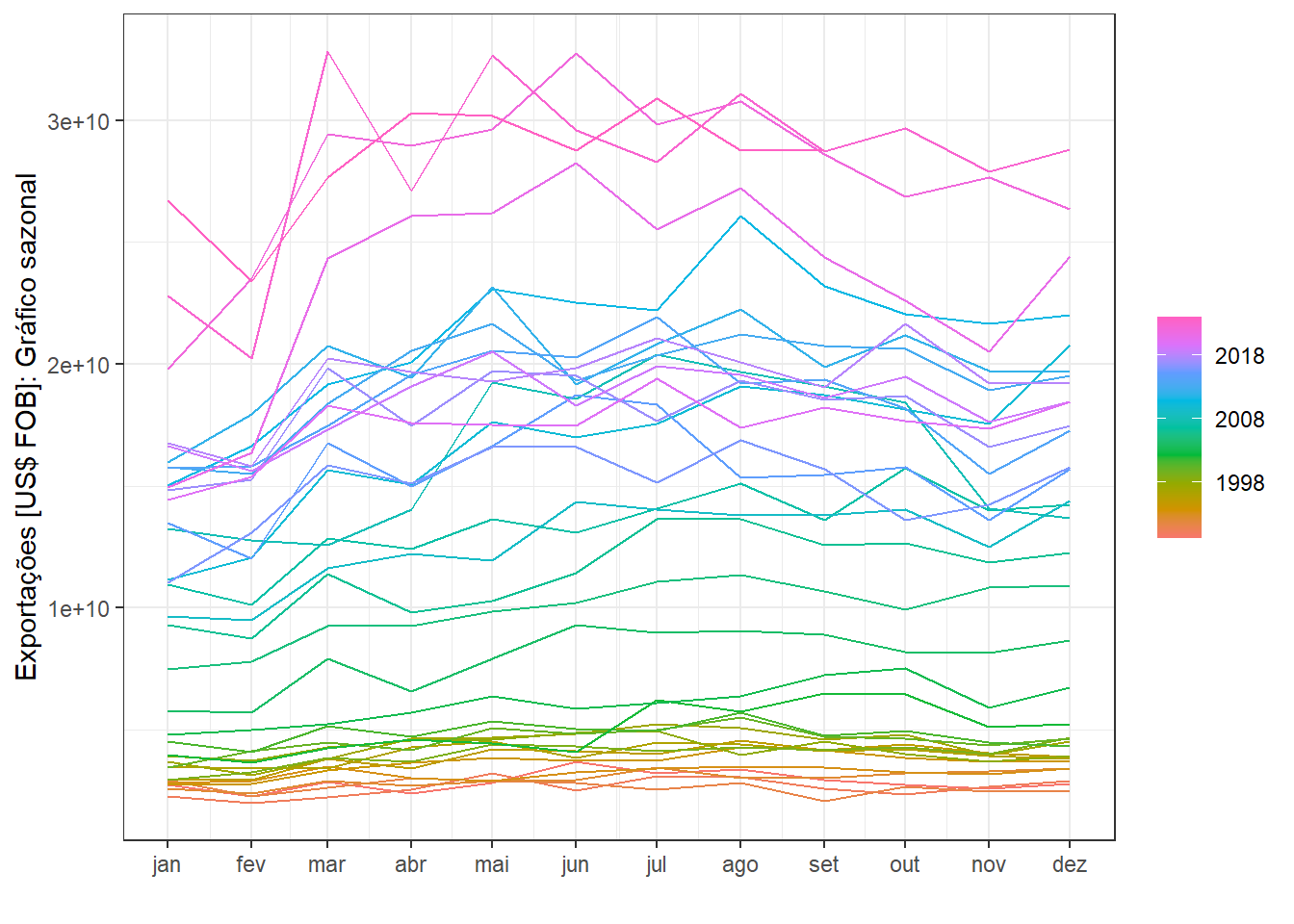
A Figura 5.8 expõe modelos de suavização exponencial com tendência e sazonalidade para a série de exportações do Brasil. Os modelos foram estimados considerando dados de até 2022, sendo as previsões plotadas 3 anos à frente. O resultado foi plotado a partir de 2020, para melhor visualização.

Figura 5.8: Modelos de suavização exponencial com tendência e sazonalidade para a série de exportações do Brasil

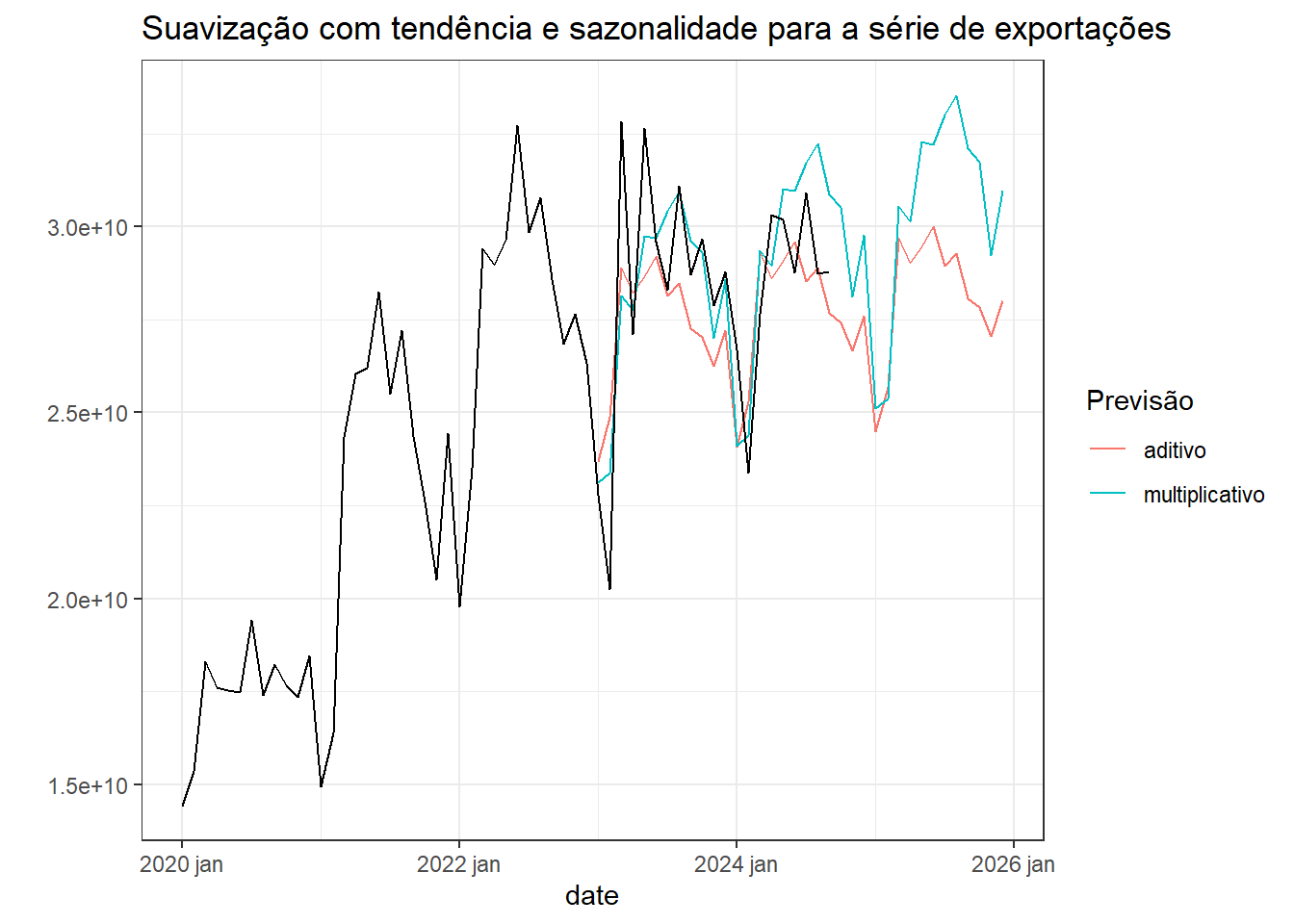
5.3.1 Suavização exponencial com tendência amortecida e sazonalidade

O método de Holt-Winters também pode considerar o amortecimento. O caso multiplicativo geralmente fornece bons resultados, sendo descrito conforme segue.

\[ \begin{align} \text{Equação de previsão: } \hat y_{t+h} &= [l_t + (\phi+\phi^2+...+\phi^h)b_t] s_{t+h-m(k+1)}\\ \text{Equação do nível: } l_t &= \alpha \frac{y_t}{s_{t-m}} + (1-\alpha)(l_{t-1}+\phi b_{t-1})\\ \text{Equação de tendência: } b_t &= \beta^*(l_t-l_{t-1})+(1-\beta^*)\phi b_{t-1}\\ \text{Equação de sazonalidade: } s_t &= \gamma \frac {y_t}{(l_{t-1}-\phi b_{t-1})}+(1-\gamma)s_{t-1}, \end{align} \]

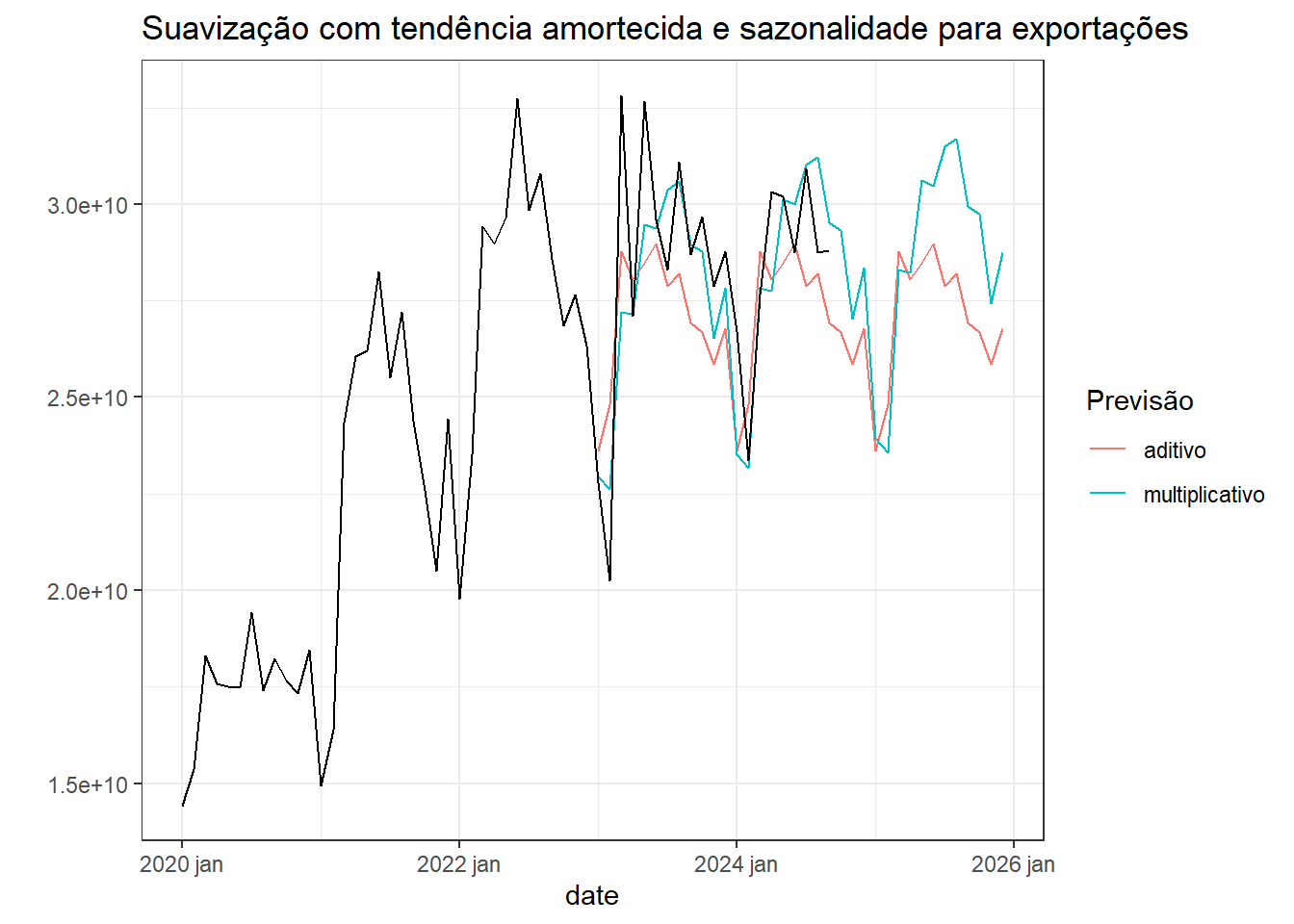
A Figura 5.9 expõe modelos de suavização exponencial com tendência amortecida e sazonalidade para a série de exportações do Brasil. O caso multiplicativo parece uma opção interessante com boa adequação aos períodos disponíveis, fazendo uma projeção à frente mais conservadora em comparação ao sem amortecimento.

Figura 5.9: Modelos de suavização exponencial com tendência amortecida e sazonalidade para a série de exportações do Brasil

5.4 Modelos de ETS e definição de espaço de estados

Os modelos de suavização exponencial podem ser concebidos como modelos de espaço de estados, com uma equação de medição que descreve os dados observados e outras de estados, por exemplo as de nível, tendência e sazonalidade, que descrevem como os componentes ou estados mudam no horizonte de tempo. Outro aspecto importante ainda não abordado é que além de considerar o erro aditivo há a possibilidade de considerar o erro multiplicativo nos modelos de suavização exponencial.

Os modelos de suavização exponencial são geralmente denotados por ETS(.,.,.) para descrever as três componentes (erro, tendência, suavização). O erro pode ser aditivo ou multiplicativo, E={A,M}. A tendência pode ser não considerada (N), aditiva (A) ou atitiva amortecida (damped) (Ad), T ={N,A,Ad}. Por fim, a sazonalidade pode ser não considerada, aditiva ou multiplicativa, S={N,A,M}. Logo, há 18 modelos possíveis.

Retomando a suavização exponencial simples representada em componentes:

\[ \begin{align} \text{Equação de previsão: } \hat y_{t+h} &= l_t\\ \text{Equação de suavização: } l_t &= \alpha y_t + (1-\alpha)l_{t-1}.\\ \end{align} \]

Manipulando a Equação de suavização, tem-se:

\[ \begin{align} l_t &= l_{t-1} + \alpha(y_t-l_{t-1}) \\ &= l_{t-1} + \alpha e_t, \end{align} \]

onde \(e_t=y_t-l_{t-1}=y_t - \hat{y}_{t|t-1}\) é o resíduo no tempo \(t\). Pode-se, portanto, considerar que a observação de treino é igual ao nível anterior mais o erro, \(y_t=l_{t-1}+e_t\). Logo, deve-se assumir os resíduos como ruído branco, \(e_t = \varepsilon_t \sim NID(0,\sigma_\varepsilon^2)\) ou normalmente e identicamente distribuídos.

Quando o erro é multiplicativo no caso simples tem-se \(e_t=(y_t - \hat{y}_{t|t-1})/\hat{y}_{t|t-1}\).

A título de exemplo serão apresentados os modelos Holt-Winters aditivos com erro aditivo ETS(A,A,A) e multiplicativo ETS(M,A,A).

5.4.1 Modelo de Holt-Winters aditivo, ETS(A,A,A)

Para este caso, considerando o erro igual a \(\varepsilon_t =y_t - l_{t-1} + b_{t-1} + s_{t-m}\), tem-se o modelo a seguir:

\[ \begin{align} y_t &= l_{t-1} + b_{t-1} + s_{t-m} + \varepsilon_t\\ l_t &= l_{t-1}+b_{t-1}+ \alpha \varepsilon_t\\ b_t &=b_{t-1} + \beta\varepsilon_t \\ s_t &= s_{t-m} + \gamma\varepsilon_t, \\ \end{align} \]

onde \(\beta=\beta^*\alpha\).

5.4.2 Modelo de Holt-Winters multiplicativo, ETS(M,A,A)

Para o caso com erro multiplicativo o erro com tendência e sazonalidade aditiva, o erro é calculado conforme segue:

\[ e_t= \frac{y_t - (l_{t-1} + b_{t-1} + s_{t-m})}{(l_{t-1} + b_{t-1} + s_{t-m} )} \]

O modelo fica conforme segue:

\[ \begin{align} y_t &= (l_{t-1} + b_{t-1} + s_{t-m} ) (1+\varepsilon_t)\\ l_t &= l_{t-1}+b_{t-1}+ \alpha (l_{t-1}-b_{t-1}-s_{t-m})\varepsilon_t\\ b_t &=b_{t-1} + \beta(l_{t-1} + b_{t-1} + s_{t-m} ) \varepsilon_t \\ s_t &= s_{t-m} + \gamma(l_{t-1} + b_{t-1} + s_{t-m} ) \varepsilon_t\\ \end{align} \] Aqui foram apresentados apenas alguns modelos, sendo dois deles explicitados em notação de espaço de estados. RJ Hyndman e Athanasopoulos (2021) explicitam todos os 18 modelos possíveis de suavização exponencial com a notação de estado de espaços.

5.5 Previsão e intervalo de confiança com ETS

A previsão com modelos de ETS pode ser realizada iterando as equações à frente, \(t=T+1, ..., T+h\). Por exemplo, para o modelo ETS(M,A,A) a previsão para o primeiro período não disponível seria \(\hat y_T+1 = l_{T} + b_{T} + s_{T}\).

O intervalo de confiança pode ser calculado conforme já exposto anteriormente, \(\hat{y}_{T+h|T} \pm1,96 \hat\sigma_h\), com 1,96 sendo o valor do quantil da distribuição \(z\) para 0,95 de confiança. O desvio-padrão depende do método ETS usado e a estimativa é bastante complexa. Rob Hyndman et al. (2008) fornece os cálculos detalhados.

A Figura 5.10 apresenta o fluxo de veículos no kilômetro 579 da BR040 em Minas Gerais de 01/03 a 07/04/2019, considerando os dois sentidos de circulação. A série está disponível em DNIT. Observa-se uma sazonalidade semanal e diária na série, com fluxo distinto nos dias 3 e 4 de março devido ao carnaval.

Figura 5.10: Fluxo de veículos na BR040 no kilômetro 579 de 01/03 a 07/04/2019

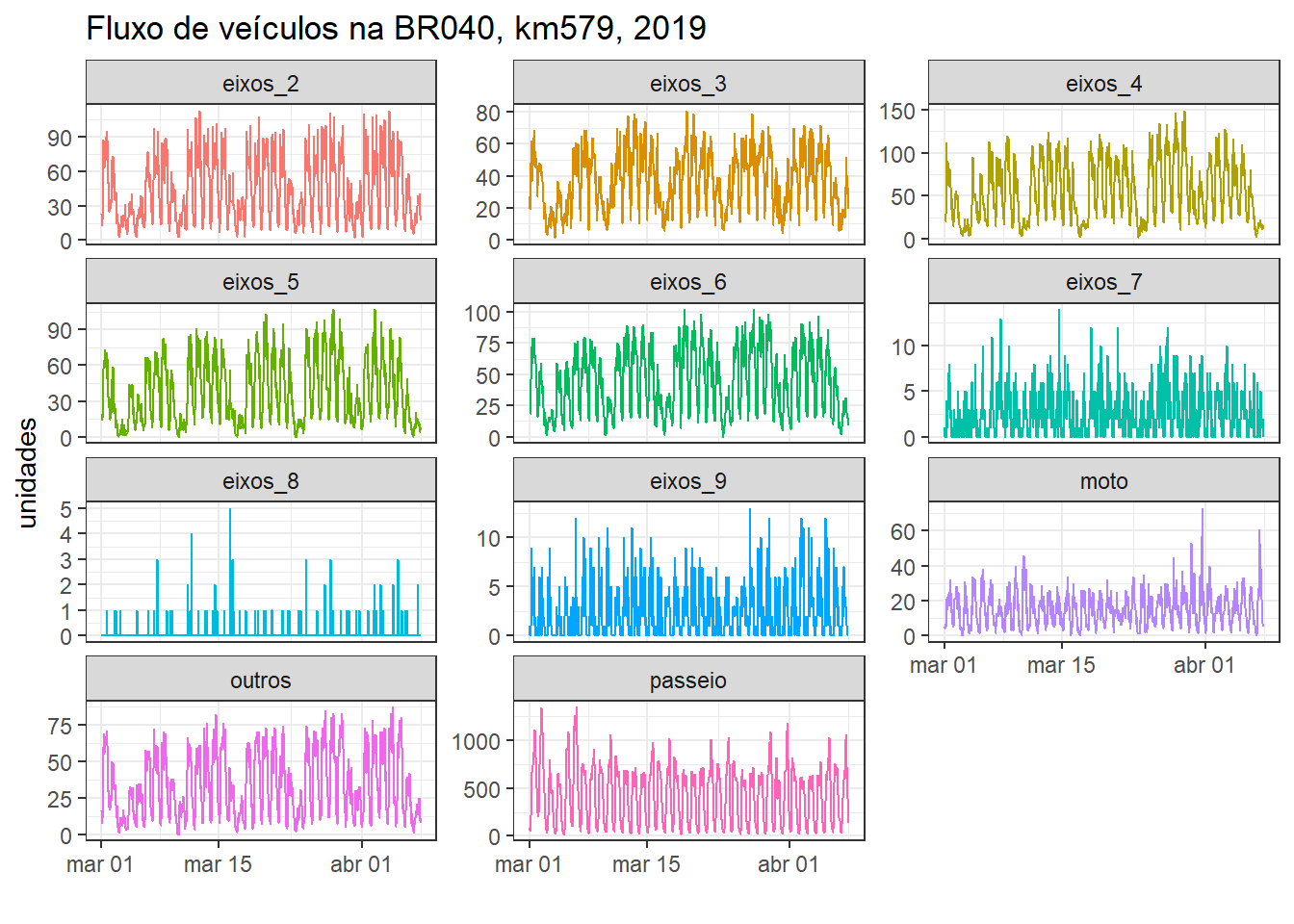
A Figura 5.11 plota a série apenas para os carros de passeio a partir de 11 de março, primeira semana após a do carnaval de 2019. Observa-se regularidade no fluxo e pico nas sextas e domingos.

Figura 5.11: Fluxo de carros de passeio na BR040 no kilômetro 579 de 01/03 a 07/04/2019

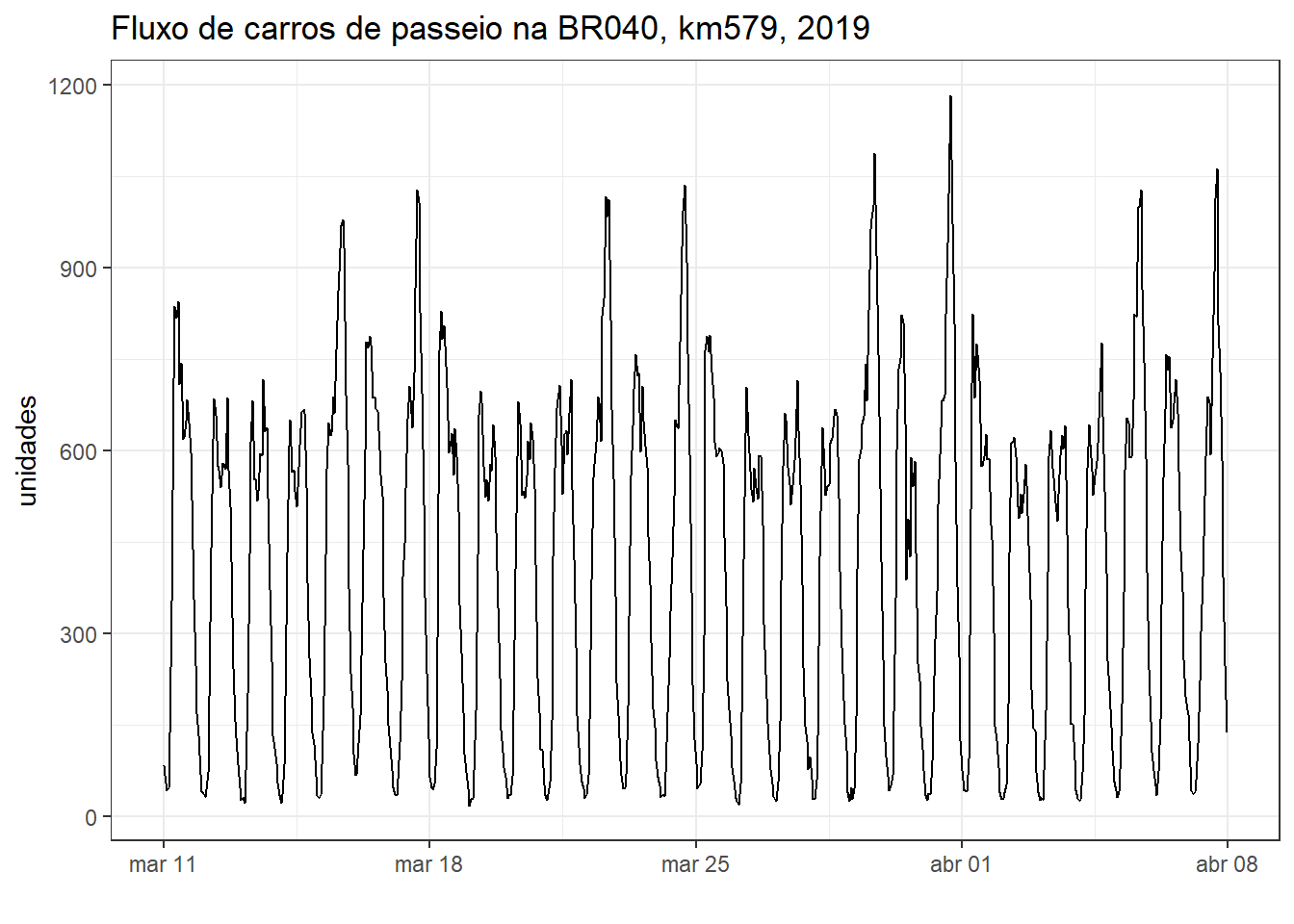
A Figura 5.12 expõe o gráfico sazonal da série anterior considerando a semana como período sazonal. Enfatiza-se a regularidade entre as 4 semanas disponíveis e observa-se novamente o pico de fluxo nas sextas e domingos devido idas e retornos de fins de semana.

Figura 5.12: Gráfico sazonal semanal do fluxo de carros de passeio na BR040 no kilômetro 579 de 01/03 a 07/04/2019

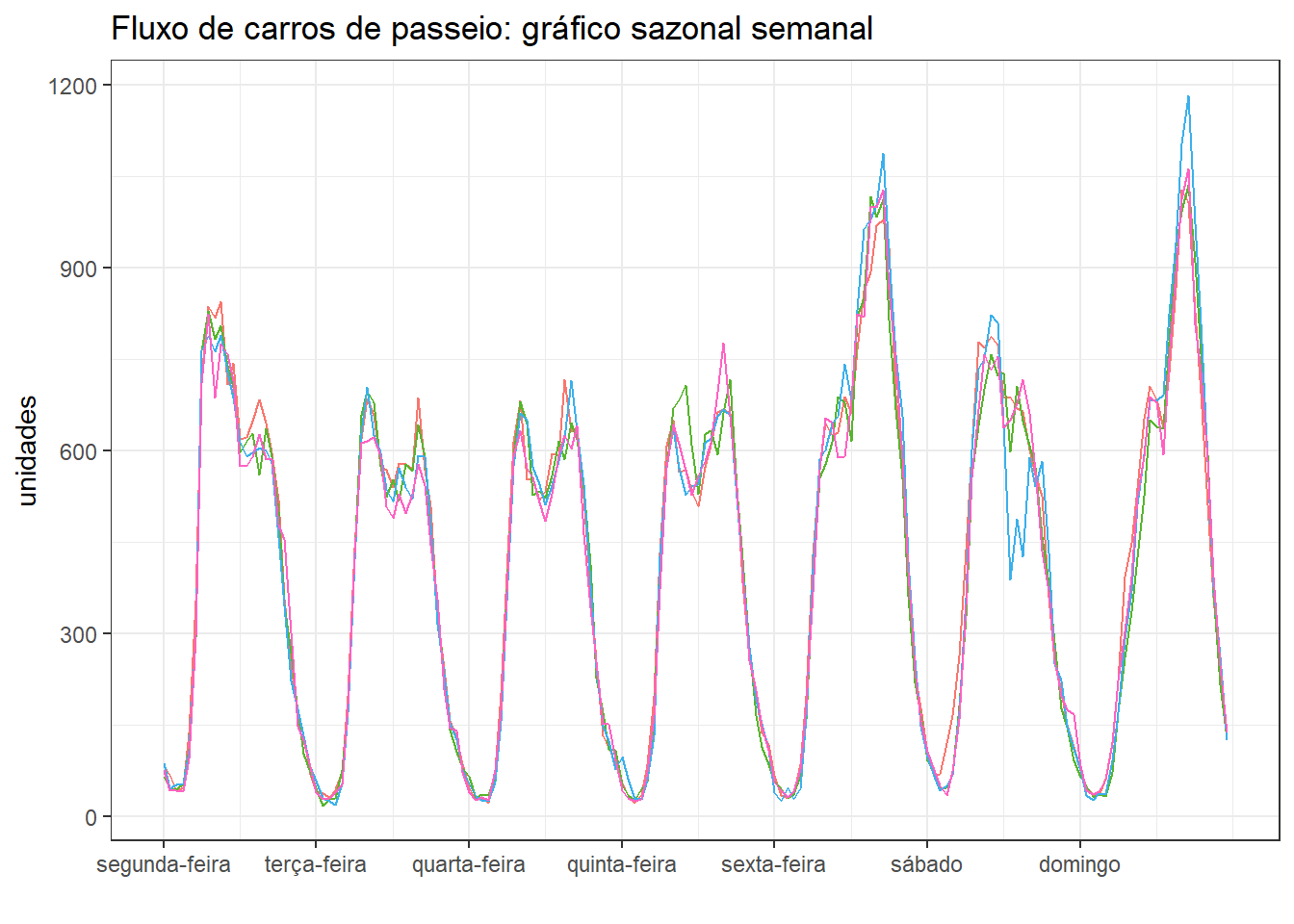
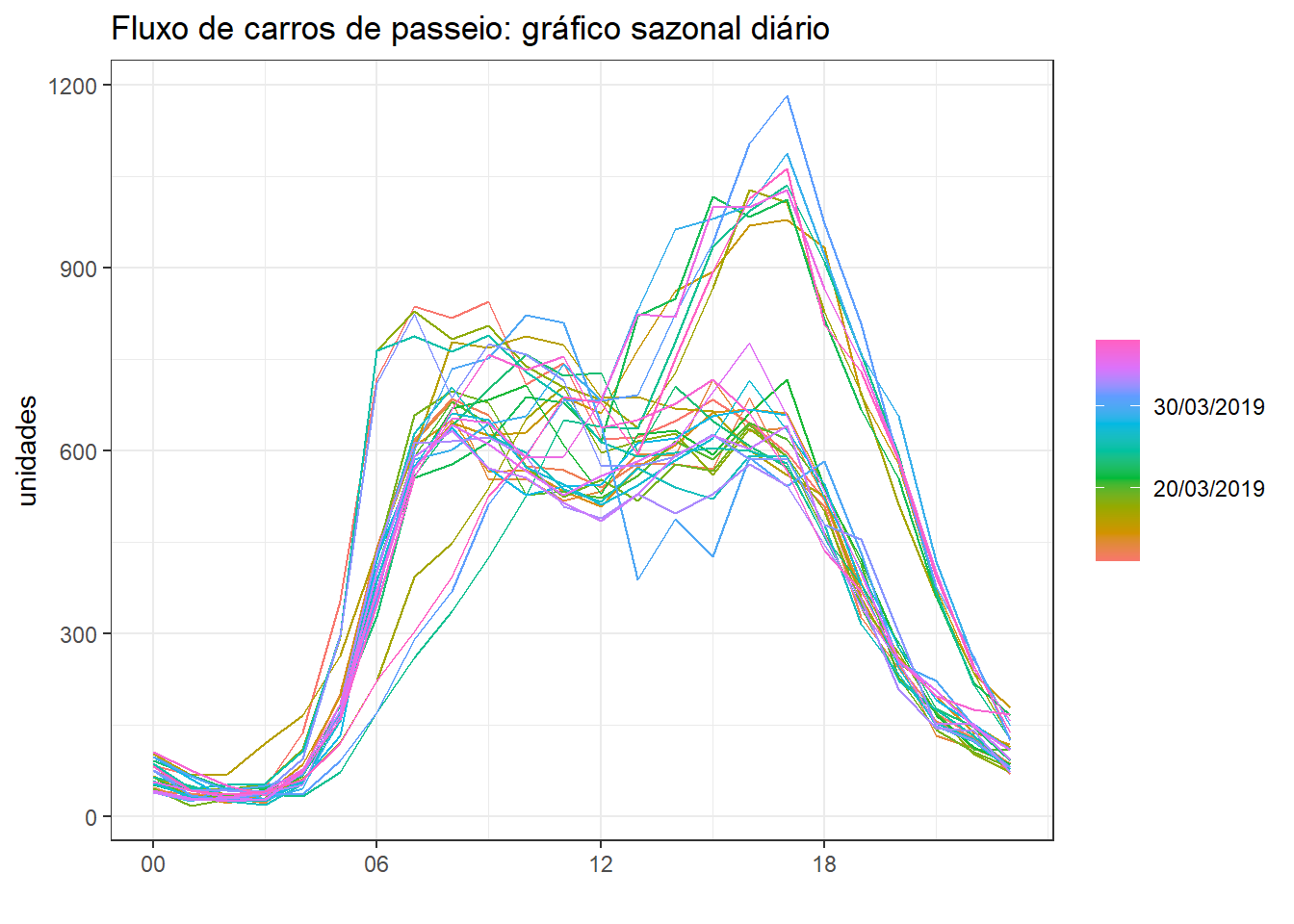
A Figura 5.13 expõe o gráfico sazonal diário do fluxo de veículos na via e kilômetro considerados. Observa-se fluxo mínimo de 0 às 4h da manhã e máximo de 7 às 17h na maior parte dos dias. Nas segundas-feiras observa-se um fluxo maior a partir das 6 da manhã. Nas sextas e domingos observa-se um fluxo maior entre as 12 e 18h.

Figura 5.13: Gráfico sazonal diário do fluxo de carros de passeio na BR040 no kilômetro 579 de 01/03 a 07/04/2019

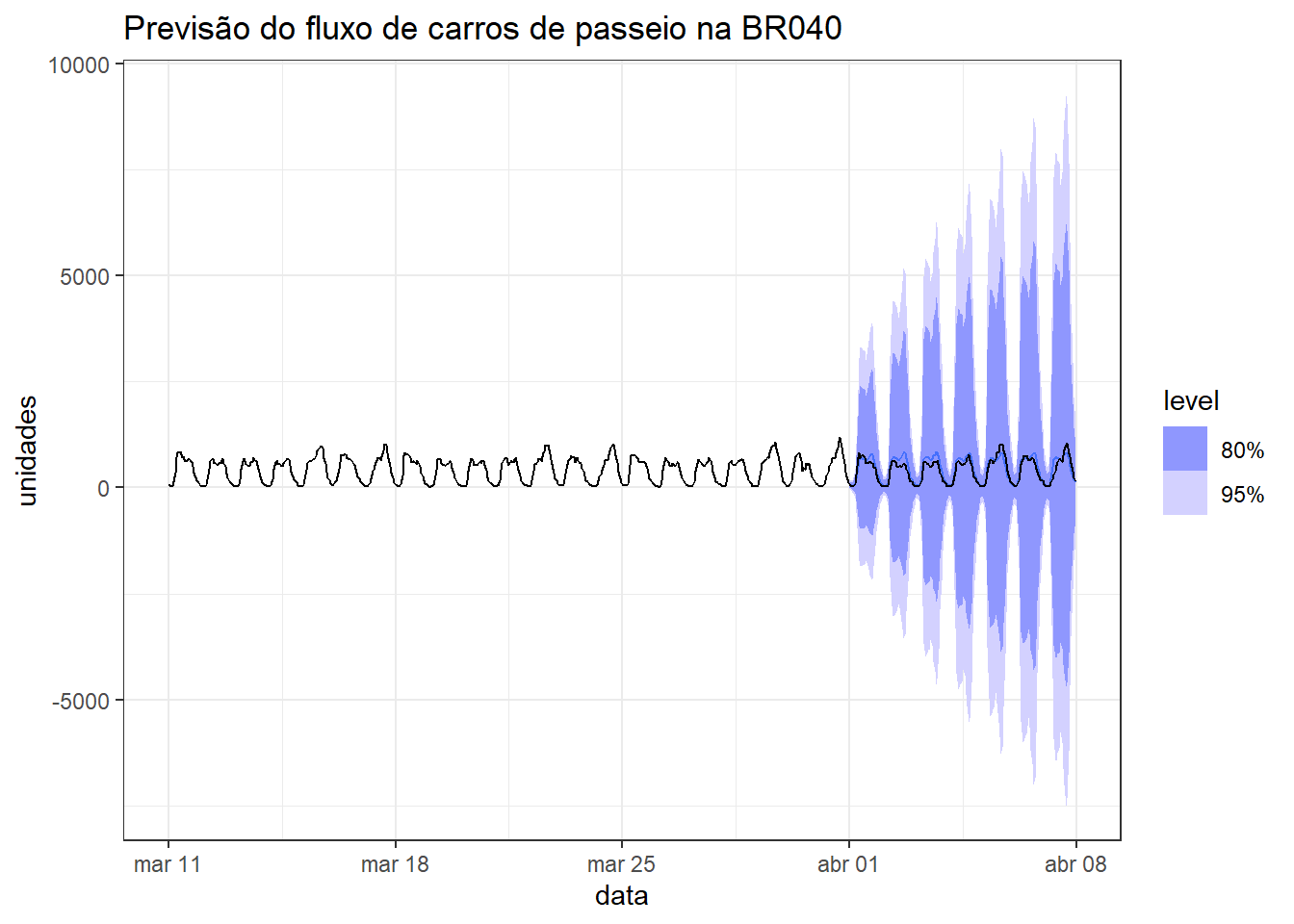
A Figura 5.14 expõe o resultado do modelo de suavização exponencial com tendência amortecida e sazonalidade. Foram considerados os dias de março para estimativa e a série completa é plotada juntamente com a previsão para a primeira semana de abril. Será importante avaliar posteriormente métodos que capturem variações sazonais distintas.

Figura 5.14: Previsão do fluxo de carros de passeio na BR040 no kilômetro 579 para a primeira semana de abril

5.6 Implementação em R

A seguir são apresentadas boa parte das implementações na linguagem R para obter os dados, gráficos e análises expostos no presente capítulo.

Carregando pacotes.

library(ggplot2)
library(tsibble)
library(fpp3)
library(rbcb)
library(knitr)
theme_set(theme_bw())

Série do IPCA.

ipca <- get_series(c(IPCA = 433), as = "ts")

ipca_tsibble <- as_tsibble(ipca, index = index)

IPCA a partir de 2019.

ipca_2019_ <- ipca_tsibble |> 
  filter(year(index) >= 2019)

Modelo de suavização exponencial simples para a série do IPCA.

fit <- ipca_2019_  |>
  model(ETS(value ~ error("A") + trend("N") + season("N")))

tidy(fit)[,-1]

Previsão 5 meses à frente.

fc <- fit |>
  forecast(h = 5)
fc

Plotando a série com os valores ajustados e a previsão.

fc |> 
  autoplot(ipca_2019_) +
  geom_line(aes(y = .fitted), col="orangered",
            data = augment(fit)) +
  labs(y = "IPCA", x = "", 
        title="IPCA no Brasil a partir de 2019") +
  guides(colour = "none")

Valores ajustados e observados para os últimos meses da série.

fit[[1]][[1]]$fit$est[,-4] |> tail()

População projetada no Brasil.

pop_br <- read.csv("populacao_br.csv", header=T)
pop_br <- pop_br |> filter(ano<=2010)

pop_ts <- pop_br |>
  mutate(data = year(as.Date(as.character(ano),format="%Y"))) |>
  select(-ano) |>
  as_tsibble(index=data)

pop_ts |> autoplot(pop) +
  labs(title = "População projetada do Brasil",
       y = "Pessoas", x="")

Modelo de suavização exponencial com tendência (método de Holt).

fit <- pop_ts |>
  model(
    AAN = ETS(pop ~ error("A") + trend("A") + season("N"))
  )

tidy(fit)

Previsão com modelos de Holt e Holt amortecido.

pop_ts |>
  model(
    `Holt` = ETS(pop ~ error("A") +
                       trend("A") + season("N")),
    `Holt amortecido` = ETS(pop ~ error("A") +
                       trend("Ad", phi = 0.9) + season("N"))
  ) |>
  forecast(h = 15) |>
  autoplot(pop_ts, level = NULL) +
  labs(title = "População do Brasil",
       y = "Milhões",x="") +
  guides(colour = guide_legend(title = "Forecast"))

Série de emissões de CO2 pela indústria.

emissoes <- read.csv("SEEG_emissoes.csv", header=T)

emissoes_ts <- emissoes |>
  pivot_longer(Mudanca.de.Uso.da.Terra.e.Floresta:Processos.Industriais) |>
  mutate(Ano = year(as.Date(as.character(Ano), "%Y"))) |>
  as_tsibble(key=name,index=Ano)

emissoes_ind<- emissoes_ts |> 
  filter(name == "Processos.Industriais")

emissoes_ind |>
  model(
    `Holt` = ETS(value ~ error("A") +
                       trend("A") + season("N")),
    `Holt amortecido` = ETS(value ~ error("A") +
                       trend("Ad", phi = 0.95) + season("N"))
  ) |>
  forecast(h = 15) |>
  autoplot(emissoes_ind , level = NULL) +
  labs(title = "Emissões de gases de efeito estufa pela indústria",
       y = "GWP",x="") +
  guides(colour = guide_legend(title = "Forecast"))

Série de exportações do Brasil.

export <- read.csv("exportacoes_BR.csv",header=T)

exp_ts <- export |>
  mutate(date = make_yearmonth(year=ano, month=mes)) |>
  select(!c(ano,mes)) |>
  as_tsibble(index=date)

exp_ts |> 
  autoplot(Exp) +
  labs(x="",y="Exportações [US$ FOB]")

Gráfico sazonal da série.

exp_ts |> gg_season(Exp) +
  labs(x="",y="Exportações [US$ FOB]: Gráfico sazonal")

Modelos de suavização exponencial com sazonalidade aditiva e multiplicativa para exportações.

fit_export <- exp_ts |> 
  filter(year(date) <=2022) |>
  model(
    aditivo = ETS(Exp ~ error("A") + trend("A") +
                                                season("A")),
    multiplicativo = ETS(Exp ~ error("M") + trend("A") +
                                                season("M"))
  )
fc_export <- fit_export |> forecast(h = "3 years")
fc_export |>
  autoplot(exp_ts |> 
  filter(year(date) >=2020), level = NULL) +
  labs(title="Suavização com tendência e sazonalidade para a série de exportações",
       y="") +
  guides(colour = guide_legend(title = "Previsão"))

Suavização exponencial com tendência amortecida e sazonalidade (aditiva e multiplicativa).

fit_export2 <- exp_ts |> 
  filter(year(date) <=2022) |>
  model(
    aditivo2 = ETS(Exp ~ error("A") + trend("Ad") +
                                                season("A")),
    multiplicativo2 = ETS(Exp ~ error("M") + trend("Ad") +
                                                season("M"))
  )
fc_export2 <- fit_export2 |> forecast(h = "3 years")
fc_export2 |>
  autoplot(exp_ts |> 
  filter(year(date) >=2020), level = NULL) +
  labs(title="Suavização com tendência amortecida e sazonalidade para exportações",
       y="") +
  guides(colour = guide_legend(title = "Previsão"))

Série de fluxo de veículos na BR 040 no kilômetro 579 de março a abril de 2019.

BR040_km_579_mar_abr <- read.csv("BR040_km_579_mar_abr.csv")

BR040_km_579_mar_abr <- BR040_km_579_mar_abr |>
  mutate(mes = c(rep(3,31*24*3),rep(4,7*24*3))) |>
  pivot_longer(eixos_2:outros)

BR040_km_579_mar_abr <- BR040_km_579_mar_abr |> 
  mutate(data = ymd_h(paste("2019", mes, dia, hora, sep = "-"))) |>
  select(!c(dia,hora,mes)) |>
  relocate(data) |>
  as_tsibble(key=c(sentido,name),index=data)

BR040_km_579_mar_abr |> filter(sentido=="Total") |> 
  select(-sentido) |>
  filter_index("2019-03-01" ~ .) |>
  autoplot(value) +
  facet_wrap(nrow=4, ~ name, scales = "free_y") +
  guides(colour = "none") + labs(x="",
                                 y="unidades",
                                 title="Fluxo de veículos na BR040, km579, 2019")

Plotando a série de carros de passeio.

passeio <- BR040_km_579_mar_abr |> filter(sentido=="Total") |> 
  select(-sentido) |>
  filter_index("2019-03-11" ~ .) |>
  filter(name=="passeio") |>
  select(-name)

passeio |>
  autoplot(value) +
  guides(colour = "none") + labs(x="",
                                 y="unidades",
                                 title="Fluxo de carros de passeio na BR040, km579, 2019")

Sazonalidade semanal.

passeio |>
  gg_season(value, period = "week", 
            labels="none") +
  labs(x="", y="unidades",
       title="Fluxo de carros de passeio: gráfico sazonal semanal")

Sazonalidade diária.

passeio |>
  gg_season(value, period = "day", 
            labels="none") +labs(x="", y="unidades",
       title="Fluxo de carros de passeio: gráfico sazonal diário", y="unidades")

Modelo de suavização exponencial com erro aditivo e sazonalidade multiplicativa.

passeio |> filter(month(data)==3) |>
  model(
    hw = ETS(value ~ error("A") + trend("N") + season("M"))
  ) |>
  forecast(h = "1 weeks", level = 80) |>
  autoplot(passeio) +
  labs(title = "Previsão do fluxo de carros de passeio na BR040",
       y="unidades")

5.7 Exercícios propostos

1. Seja a série de produção de grãos. Separe os últimos cinco anos para testar o modelo. Aplique um modelo de suavização exponencial com tendência. Considere também o caso amortecido com \(\phi = 0,9\) e \(\phi=0,95\). Avalie os resíduos dos modelos obtidos. Calcule as métricas de ajuste para os dados de teste e escolha o melhor modelo.

2. Seja a série de volume de exportações do Brasil exposta neste capítulo. Considerando os modelos obtidos de suavização exponencial com sazonalidade aditiva e multiplicativa e com tendência simples ou amortecida, avalie os resíduos de todos os modelos. Calcule as métricas de teste para os dados de 2023 à frente e escolha o melhor modelo.

3. Seja a série de fluxo de caminhões de 2 eixos no quilômetro 579 da BR040 para ambos os sentidos. Considere os dados de 11 a 31 de Março para treinar modelos de suavização exponencial sem tendência com sazonalidade e erro aditivos e multiplicativos. Avalie os resíduos dos modelos. Exclua algum modelo com problemas maiores nos resíduos e teste os modelos com os dados disponíveis de abril e selecione o melhor modelo.

Gardner, Everette S., e Ed. Mckenzie. 1985. «Forecasting Trends in Time Series». Management Science 31 (10): 1237–46. https://doi.org/10.1287/mnsc.31.10.1237.

Holt, Charles C. 2004. «Forecasting seasonals and trends by exponentially weighted moving averages». International Journal of Forecasting 20 (1): 5–10. https://doi.org/https://doi.org/10.1016/j.ijforecast.2003.09.015.

Hyndman, RJ, e G Athanasopoulos. 2021. Forecasting: principles and practice. OTexts. OTexts.com/fpp3.

Hyndman, Rob, Anne B Koehler, J Keith Ord, e Ralph D Snyder. 2008. Forecasting with exponential smoothing: the state space approach. Springer Science & Business Media.

Winters, Peter R. 1960. «Forecasting Sales by Exponentially Weighted Moving Averages». Management Science 6 (3): 324–42. https://doi.org/10.1287/mnsc.6.3.324.